Die Graphen von \(h_k\) und \(h'_k\) werden in der Abbildung 3 für \(k = 4\) beispielhaft für gerade Werte von \(k\) gezeigt, in der Abbildung 4 für \(k = 5\) beispielhaft für ungerade Werte von \(k\). Für \(k \geq 4\) werden die Punkte \(P(4|h_k(4))\), \(Q(4|h'_k(4))\), \(R(2|h_k(2))\) und \(S(2|h'_k(2))\) betrachtet. Diese Punkte sind jeweils Eckpunkte eines Vierecks.
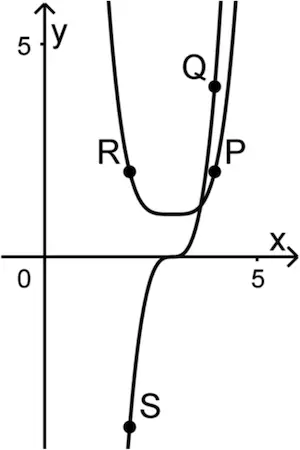Abb. 3
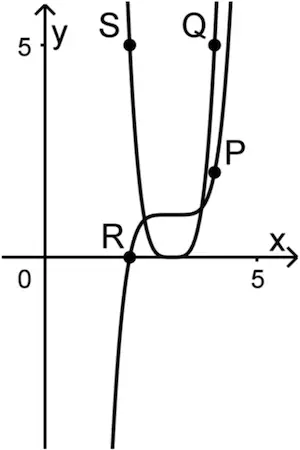Abb. 4
Begründen Sie dass jedes dieser Vierecke ein Trapez ist, und zeigen Sie, dass die folgende Aussage richtig ist:
Für jeden geraden Wert von \(k\) mit \(k \geq 4\) stimmen der Flächeninhalt des Trapezes für \(k\) und der Flächeninhalt des Trapezes für \(k + 1\) überein.
(7 BE)
Lösung zu Teilaufgabe 2d
Begründung, weshalb jedes der Vierecke ein Trapez ist
Da die Punkte \(P(\textcolor{#e9b509}{4}|h_k(4))\) und \(Q(\textcolor{#e9b509}{4}|h'_k(4))\) sowie die Punkte \(R(\textcolor{#e9b509}{2}|h_k(2))\) und \(S(\textcolor{#e9b509}{2}|h'_k(2))\) jeweils in den \(\textcolor{#e9b509}{x}\)-Koordinaten übereinstimmen, sind die Seiten \(\boldsymbol{[PQ]}\) und \(\boldsymbol{[RS]}\) zueinander parallel und die Vierecke sind somit Trapeze.
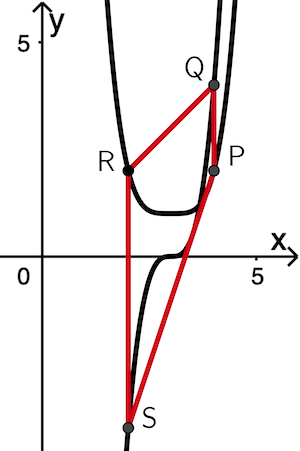Abb. 3
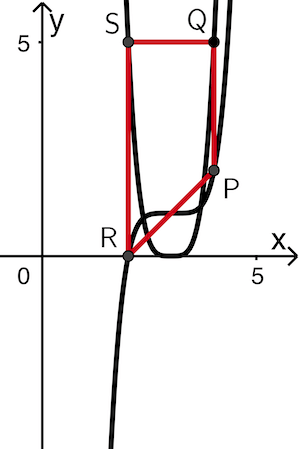Abb. 4
Nachweis, dass folgende Aussage richtig ist
Für jeden geraden Wert von \(k\) mit \(k \geq 4\) stimmen der Flächeninhalt des Trapezes für \(k\) und der Flächeninhalt des Trapezes für \(k + 1\) überein.
Anmerkung
Der Nachweis ist übersichtlicher zu führen, wenn zuerst die \(y\)-Koordinaten der Eckpunkte der Trapeze für gerade Werte von \(k\) und für ungerade Werte \(k + 1\) bestimmt werden.
\[h_k(x) = (x - 3)^k + 1\]
\[h'_k(x) = k \cdot (x - 3)^{k - 1}\]
\(y\)-Koordinaten der Eckpunkte für gerade Werte von \(\boldsymbol{k}\) mit \(k \geq 4\)
\(P(4|h_k(4))\)
\[\begin{align*}h_k(4) &= (4 - 3)^k + 1 = 1^k + 1 \\[0.8em] &= 1 + 1 = 2 \; \Rightarrow \; P(4|2)\end{align*}\]
\(Q(4|h'_k(4))\)
\[\begin{align*}h'_k(4) &= k \cdot (4 - 3)^{k - 1} = k \cdot 1^{k - 1} \\[0.8em] &= k \cdot 1 = k\;\Rightarrow\; Q(4|k)\end{align*}\]
\(R(2|h_k(2))\)
\[\begin{align*}h_k(2) &= (2 - 3)^k + 1 = (-1)^k + 1 \\[0.8em] &= 1 + 1 = 2 \; \Rightarrow \; R(2|2)\end{align*}\]
\(S(2|h'_k(2))\)
\[\begin{align*}h'_k(2) &= k \cdot (2 - 3)^{k - 1} = k \cdot (-1)^{k - 1} \\[0.8em] &= k \cdot (-1) = -k \;\Rightarrow\; S(2|-k)\end{align*}\]
\(y\)-Koordinaten der Eckpunkte für ungerade Werte \(\boldsymbol{k + 1}\)
\(P(4|h_k(4))\)
\[\begin{align*}h_{k \,+\, 1}(4) &= (4 - 3)^{k + 1} + 1 = 1^{k\, +\, 1} + 1 \\[0.8em] &= 1 + 1 = 2 \; \Rightarrow \; P(4|2)\end{align*}\]
\(Q(4|h'_k(4))\)
\[\begin{align*}h'_{k \,+\, 1}(4) &= (k + 1) \cdot (4 - 3)^{k \,+\, 1\, - 1} = (k + 1) \cdot 1^{k} \\[0.8em] &= (k + 1) \cdot 1 = k + 1\;\Rightarrow\; Q(4|k + 1)\end{align*}\]
\(R(2|h_k(2))\)
\[\begin{align*}h_{k\,+\,1}(2) &= (2 - 3)^{k \,+\,1} + 1 = (-1)^{k\, +\, 1} + 1 \\[0.8em] &= -1 + 1 = 0 \; \Rightarrow \; R(2|0)\end{align*}\]
\(S(2|h'_k(2))\)
\[\begin{align*}h'_{k\,+\,1}(2) &= (k + 1) \cdot (2 - 3)^{k\, +\, 1\, - 1} = (k + 1) \cdot (-1)^{k} \\[0.8em] &= (k + 1) \cdot 1 = k + 1 \;\Rightarrow\; S(2|k + 1)\end{align*}\]
Flächeninhalte der Trapeze berechnen
Die Längen der parallelen Seiten lassen sich als Differenz der \(y\)-Koordinaten der entsprechenden Punkte berechnen. Die Höhe der Trapeze ist gleich dem Abstand der parallelen Seiten. Sie lässt sich beispielsweise als Differenz der \(x\)-Koordinaten der Punkte \(P\) und \(R\) berechnen.
Flächeninhalt eines Trapezes
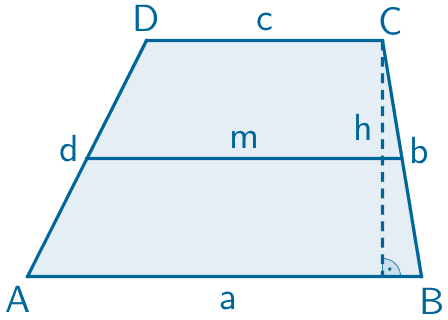
\[A = m \cdot h = \frac{a + c}{2} \cdot h\]
Flächeninhalt des Trapez \(RSPQ\) für gerade Werte von \(\boldsymbol{k}\) (vgl. Abbildung 3):
Eckpunkte: \(P(\textcolor{#e9b509}{4}|\textcolor{#0087c1}{2})\), \(Q(\textcolor{#e9b509}{4}|\textcolor{#0087c1}{k})\), \(R(\textcolor{#e9b509}{2}|\textcolor{#0087c1}{2})\) und \(S(\textcolor{#e9b509}{2}|\textcolor{#0087c1}{-k})\)
\[\begin{align*}A_{RSPQ} &= \frac{1}{2} \cdot \Big( \overline{RS} + \overline{QP} \Big) \cdot h \\[0.8em] &= \frac{1}{2} \cdot [(\textcolor{#0087c1}{y_R} - \textcolor{#0087c1}{y_S}) + (\textcolor{#0087c1}{y_Q} - \textcolor{#0087c1}{y_P})] \cdot (\textcolor{#e9b509}{x_P} - \textcolor{#e9b509}{x_R}) \\[0.8em] &= \frac{1}{2} \cdot [(\textcolor{#0087c1}{2} - \textcolor{#0087c1}{(-k)})+(\textcolor{#0087c1}{k} - \textcolor{#0087c1}{2})] \cdot (\textcolor{#e9b509}{4} - \textcolor{#e9b509}{2}) \\[0.8em] &= \frac{1}{2} \cdot (2 + k + k -2) \cdot 2 \\[0.8em] &= 2k\end{align*}\]
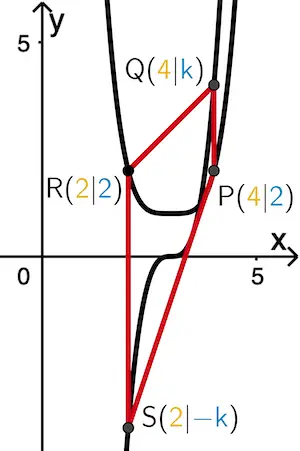Abb. 3
Flächeninhalt des Trapez \(RSPQ\) für ungerade Werte \(\boldsymbol{k + 1}\) (vgl. Abbildung 4):
Eckpunkte: \(P(\textcolor{#e9b509}{4}|\textcolor{#0087c1}{2})\), \(Q(\textcolor{#e9b509}{4}|\textcolor{#0087c1}{k+1})\), \(R(\textcolor{#e9b509}{2}|\textcolor{#0087c1}{0})\) und \(S(\textcolor{#e9b509}{2}|\textcolor{#0087c1}{k+1})\)
\[\begin{align*}A_{SRPQ} &= \frac{1}{2} \cdot \Big( \overline{SR} + \overline{QP} \Big) \cdot h \\[0.8em] &= \frac{1}{2} \cdot [(\textcolor{#0087c1}{y_S} - \textcolor{#0087c1}{y_R}) + (\textcolor{#0087c1}{y_Q} - \textcolor{#0087c1}{y_P})] \cdot (\textcolor{#e9b509}{x_P} - \textcolor{#e9b509}{x_R}) \\[0.8em] &= \frac{1}{2} \cdot [(\textcolor{#0087c1}{k+1} - \textcolor{#0087c1}{0})+(\textcolor{#0087c1}{k+1} - \textcolor{#0087c1}{2})] \cdot (\textcolor{#e9b509}{4} - \textcolor{#e9b509}{2}) \\[0.8em] &= \frac{1}{2} \cdot (k + 1 + k - 1) \cdot 2 \\[0.8em] &= 2k\end{align*}\]
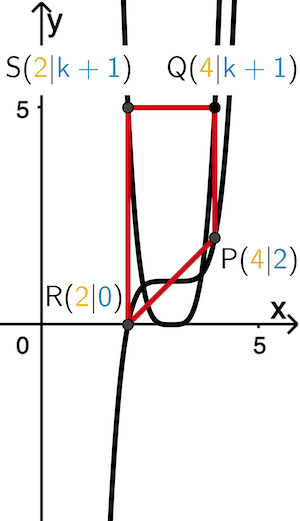Abb. 4
Somit ist die Aussage
Für jeden geraden Wert von \(k\) mit \(k \geq 4\) stimmen der Flächeninhalt des Trapezes für \(k\) und der Flächeninhalt des Trapezes für \(k + 1\) überein.
richtig.
