Für das Unternehmen wäre es hilfreich, wenn die Wahrscheinlichkeit dafür, mindestens eine Person mit Reservierung abweisen zu müssen, höchstens ein Prozent wäre. Dazu müsste die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person mit Reservierung nicht zur Fahrt erscheint, mindestens einen bestimmten Wert haben. Ermitteln Sie diesen Wert auf ganze Prozent genau.
(3 BE)
Lösung zu Teilaufgabe 2c
Es sei \(Y\) die Zufallsgröße, welche die Anzahl der Personen mit Reservierung beschreibt, die abgewiesen werden müssen.
\(X\): Anzahl der Personen mit Reservierung, die nicht zur Fahrt erscheinen (vgl. Teilaufgabe 2a).
\(n = 64\)
Gesucht ist die kleinstmögliche Trefferwahrscheinlichkeit \(p\) des Ereignisses „Eine Person mit Reservierung erscheint nicht zur Fahrt.", also der kleinstmögliche Wert des Parameters \(p\) der nach \(B(64; p)\) binomialverteilten Zufallsgröße \(X\).
„Für das Unternehmen wäre es hilfreich, wenn die Wahrscheinlichkeit dafür, mindestens eine Person mit Reservierung abweisen zu müssen, höchstens ein Prozent wäre."
Betrachten des Gegenereignisses (mindestens 1 Treffer)
Wahrscheinlichkeitsberechnungen einer binomialverteilten Zufallsgröße \(X\) der Form „mindestens 1 Treffer" \(P(X \geq 1)\) vereinfachen sich durch die Betrachtung des Gegenereignisses „nicht 0 Treffer":
\[P(X \geq 1) = 1 - P(X = 0)\]
\[\begin{align*} \Longrightarrow \quad \textcolor{#cc071e}{P(Y \geq 1)} & \; \textcolor{#0087c1}{\leq 0{,}01} \\[0.8em] 1 - P(Y = 0) &\leq 0{,}01 &&| -1 \\[0.8em] -P(Y = 0) &\leq -0{,}99 &&| \cdot (-1) \; \text{Relationszeichen dreht!} \\[0.8em] P(Y = 0) &\geq 0{,}99 \end{align*}\]
Nun beschreibt \(P(Y = 0)\) die Wahrscheinlichkeit dafür, dass keine Person mit Reservierung abgewiesen werden muss. Diese Wahrscheinlichkeit wurde in Teilaufgabe 2b bereits mithilfe der Zufallsgröße \(X\) formuliert: \(P(X \geq 4)\) (Wenn mindestens 4 Personen mit Reservierung nicht erscheinen, muss keine Person mit Reservierung abgewiesen werden).
\[P(Y = 0) = P(X \geq 4)\]
Somit folgt:
Betrachten des Gegenereignisses (mindestens \(k\) Treffer)
Kumulative Wahrscheinlichkeiten der Form \(P(X \geq k)\) lassen sich im Stochastischen Tafelwerk (ST) nicht nachschlagen. Die Betrachtung des Gegenereignisses ermöglicht das Verwenden des Stochastischen Tafelwerks:
\[P(X \geq k) = 1 - P(X \leq k - 1)\]
Die Kumulative Verteilungsfunktion \(F_{p}^{n}(k) = P^n_p(X \leq k) = \sum \limits_{i\;=\;0}^{k} B(n;p;i)\) ist für bestimmte Werte der Parameter \(p\) und \(n\) in der rechten Spalte des Stochastischen Tafelwerks mit Abiturzulassung tabellarisiert.
\[\begin{align*} P_{p}^{64}(X \geq 4) &\geq 0{,}99 \\[0.8em] 1 - P_{p}^{64}(X \leq 3) &\geq 0{,}99 &&| -1 \\[0.8em] -P(X \leq 3) &\geq -0{,}01 &&| \cdot (-1) \; \text{Relationszeichen dreht!} \\[0.8em] P_{p}^{64}(X \leq 3) &\leq 0{,}01 \end{align*}\]
Mithilfe der Tabelle der Angabe ergibt sich in der Zeile \(k = 3\):
\[p = 0{,}15 = 15\,\%\]
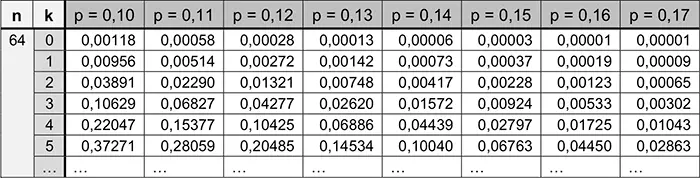
Binomialverteilung kumulativ; \(k \mapsto \sum \limits_{i\,=\,0}^{k} B(n;p;i)\)
Damit die Wahrscheinlichkeit dafür, mindestens eine Person mit Reservierung abweisen zu müssen, höchstens ein Prozent beträgt, müsste die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person mit Reservierung nicht zur Fahrt erscheint, mindestens 15 % betragen.
