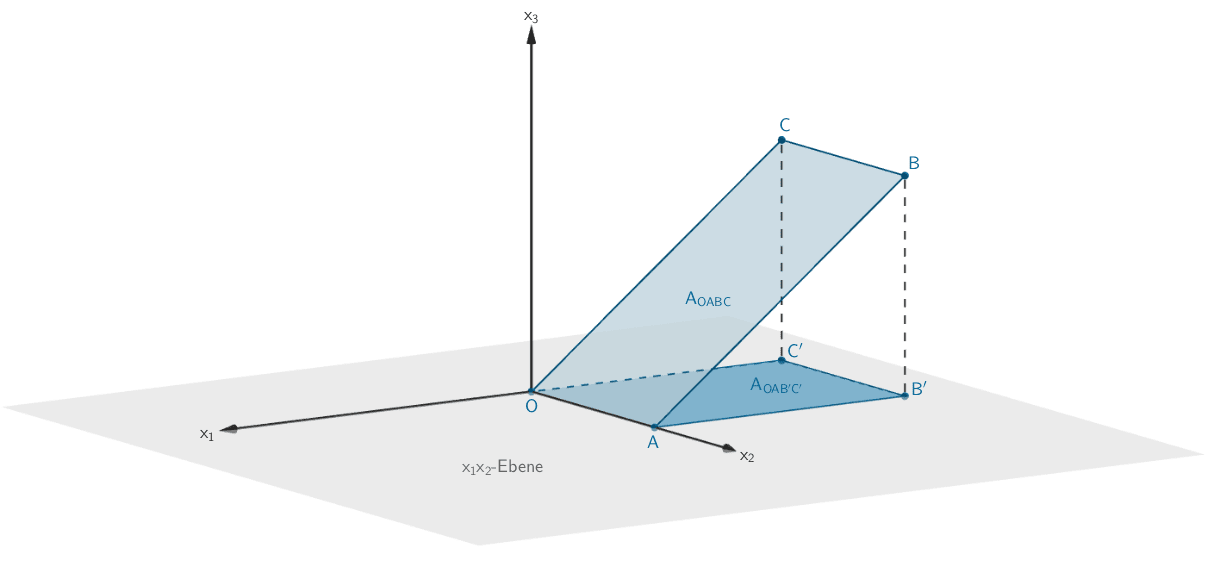
Das Rechteck \(OABC\) ist das Modell eines steilen Hanggrundstücks; die positive \(x_1\)-Achse beschreibt die südliche, die positive \(x_2\)-Achse die östliche Himmelsrichtung (im Koordinatensystem: 1 LE entspricht 1 m, d.h. die Länge des Grundstücks in West-Ost-Richtung beträgt 60 m.).
Obwohl das Rechteck \(OABC\) den Flächeninhalt 6000 besitzt, ist das Hanggrundstück auf einer Landkarte des Grundbuchamts mit einer Größe von 4800 m2 verzeichnet. Stellen Sie ausgehend von der Zeichnung aus Aufgabe b eine Vermutung an, welche sinnvolle Regelung das Grundbuchamt damit bei der Festlegung der Grundstücksgröße umsetzt. Bestätigen Sie Ihre Vermutung durch Rechnung.
(3 BE)
Lösung zu Teilaufgabe c
Vermutung: Bei der Festlegung der Grundstücksgröße wird die senkrechte Projektion eines Grundstücks auf die Horizontalebene (\(x_1x_2\)-Ebene) herangezogen. Auf der Landkarte des Grundbuchamts ist also der Flächeninhalt des Rechtecks \(OAB'C'\) verzeichnet.
\[B'(-80|60|0), \enspace C'(-80|0|0)\]
Flächeninhalt des Rechtecks \(OAB'C'\)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[ \begin {align*} A_{OAB'C'} &= \left| \overrightarrow{OA} \right| \cdot \left| \overrightarrow{OC'} \right| \\[0.8em] &= \left| \overrightarrow A \right| \cdot \left| \overrightarrow C' \right| \\[0.8em] &= \left| \begin {pmatrix} 0 \\ 60 \\ 0 \end {pmatrix} \right| \cdot \left| \begin {pmatrix} -80 \\ 0 \\ 0 \end {pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + 60^2 + 0^2} \cdot \sqrt{(-80)^2 + 0^2 + 0^2} \\[0.8em] &= 60 \cdot 80 \\[0.8em] &= 4800 \end {align*} \]
Alternativer Lösungsansatz: Anwenden des Vektorprodukts
Anwendung des Vekorprodukts
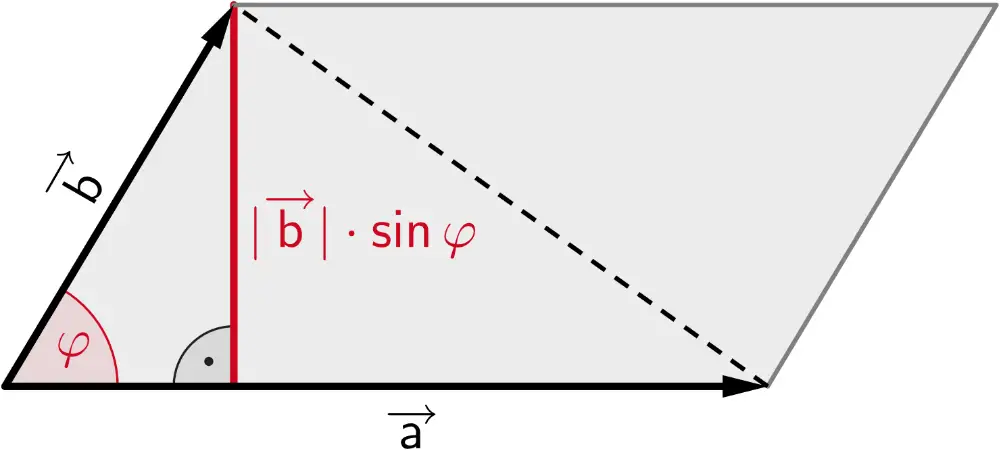
Der Betrag des Vektorprodukts \(\overrightarrow{a} \times \overrightarrow{b}\) entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren \(\overrightarrow{a} \neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\) aufgespannten Parallelogramms.
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \textcolor{#cc071e}{\vert \overrightarrow{b} \vert \cdot \sin{\varphi}}\]
Flächeninhalt eines Parallelogramms
\[A = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks
\[A = \frac{1}{2} \cdot \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
\[ \begin {align*} A_{OAB'C'} &= \left| \overrightarrow{OA} \times \overrightarrow{OC'} \right| \\[0.8em] &= \left| \overrightarrow A \times \overrightarrow C' \right| \\[0.8em] &= \left| \begin {pmatrix} 0 \\ 60 \\ 0 \end {pmatrix} \times \begin {pmatrix} -80 \\ 0 \\ 0 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 60 & \cdot & 60 & - & 0 & \cdot & 0 \\ 0 & \cdot & (-80) & - & 0 & \cdot & 0 \\ 0 & \cdot & 0 & - & 60 & \cdot & (-80) \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 0 \\ 0 \\ 4800 \end {pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + 0^2 + 4800^2} \\[0.8em] &= 4800 \end {align*} \]