Ein Autozulieferer hat zwei Betriebsstandorte A und B. Die Zahl der Beschäftigten am Standort A ist viermal so groß wie am Standort B. 60 % aller Beschäftigten des Autozulieferers haben sich für den Kauf eines Jobtickets entschieden, mit dem die Firma die Nutzung des öffentlichen Personennahverkehrs für den Weg zur Arbeit fördert.
Bestimmen Sie unter der Annahme, dass der Anteil der Beschäftigten mit einem Jobticket an beiden Standorten gleich ist, die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Beschäftigter des Autozulieferers am Standort B arbeitet und kein Jobticket besitzt.
(2 BE)
Lösung zu Teilaufgabe 3a
\[P(B \cap \overline{J}) = P(B) \cdot P(\overline{J}) = 0{,}2 \cdot 0{,}4 = 0{,}08 = 8\,\%\]
Ausführliche Lösung (nicht verlangt)
\(A\): „Beschäftigte(r) am Strandort A"
\(B\): „Beschäftigte(r) am Strandort B"
\(J\): „Beschäftigte(r) besitzt ein Jobticket."
\(\overline{J}\): „Beschäftigte(r) besitzt kein Jobticket."
Analyse der Angabe
„Die Zahl der Beschäftigten am Standort A ist viermal so groß wie am Standort B."
\(\Rightarrow\; \vert A \vert = 4 \cdot \vert B \vert\) bzw. \(P(A) = 4 \cdot P(B)\)
„60 % aller Beschäftigten des Autozulieferers haben sich für den Kauf eines Jobtickets entschieden, ..."
\(\Rightarrow\;P(J) = 0{,}6; \; P(\overline{J}) = 1 - 0{,}6 = 0{,}4\)
„Bestimmen Sie unter der Annahme, dass der Anteil der Beschäftigten mit einem Jobticket an beiden Standorten gleich ist, ..."
\(\Rightarrow\;P_A(J) = P_B(J) = P(J) = 0{,}6\)
Das bedeutet, dass die Ereignisse \(A\) und \(J\) bzw. \(B\) und \(J\) stochastisch unabhängig sind.
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
Veranschaulichung mithilfe eines Baumdiagramms
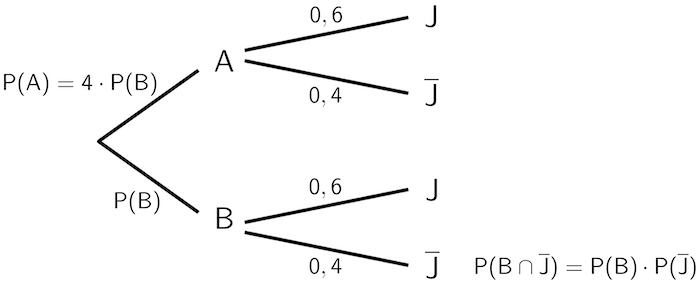
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Knotenregel anwenden:
\[\begin{align*}P(A) + P(B) &= 1 \\[0.8em] 4 \cdot P(B) + P(B) &= 1 \\[0.8em] 5 \cdot P(B) &= 1 &&| : 5 \\[0.8em] P(B) &= 0{,}2\end{align*}\]
1. Pfadregel (Produktregel) anwenden:
\[P(B \cap \overline{J}) = P(B) \cdot P(\overline{J}) = 0{,}2 \cdot 0{,}4 = 0{,}08 = 8\,\%\]
Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Beschäftigter des Autozulieferers am Standort B arbeitet und kein Jobticket besitzt, beträgt 8 %.
Alternative: Vierfeldertafel (gegeben, gesucht)
| \(A\) | \(B\) | ||
| \(J\) | \(\textcolor{#89ba17}{0{,}6}\) | ||
| \(\overline{J}\) | \(\textcolor{#cc071e}{P(B \cap \overline{J})}\) | \(0{,}4\) | |
| \(P(A) = \textcolor{#89ba17}{4\cdot P(B)}\) | \(P(B)\) | \(1\) |
\[\begin{align*}P(A) + P(B) &= 1 \\[0.8em] 4 \cdot P(B) + P(B) &= 1 \\[0.8em] 5 \cdot P(B) &= 1 &&| : 5 \\[0.8em] P(B) &= 0{,}2\end{align*}\]
| \(A\) | \(B\) | ||
| \(J\) | \(0{,}6\) | ||
| \(\overline{J}\) | \(\textcolor{#cc071e}{P(B \cap \overline{J})}\) | \(0{,}4\) | |
| \(0{,}8\) | \(0{,}2\) | \(1\) |
Da die Ereignisse \(A\) und \(J\) bzw. \(B\) und \(J\) stochastisch unabhängig sind, ist die Vierfeldertafel der Wahrscheinlichkeiten eine „Multiplikationstafel". Die Wahrscheinlichkeiten der inneren Einträge (Schnittmengen) errechnen sich als Produkt der Wahrscheinlichkeiten der zugehörigen äußeren Einträge (Ereignisse).
\[\textcolor{#cc071e}{P(B \cap \overline{J})} = P(B) \cdot P(\overline{J}) = 0{,}2 \cdot 0{,}4 = 0{,}08 = 8\,\%\]
Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Beschäftigter des Autozulieferers am Standort B arbeitet und kein Jobticket besitzt, beträgt 8 %.


