Geben Sie jeweils den Term einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt.
Die Funktion \(g\) hat die maximale Definitionsmenge \(]-\infty;5[\).
(2 BE)
Lösung zu Teilaufgabe 3a
Funktionsterm bestimmen
\[D_{g} = \; ]-\infty; 5]\]
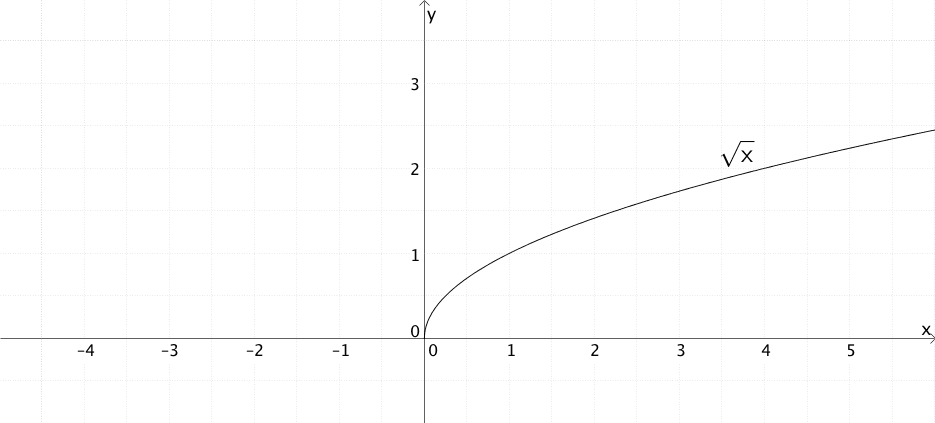
Beispiel Wurzelfunktion:
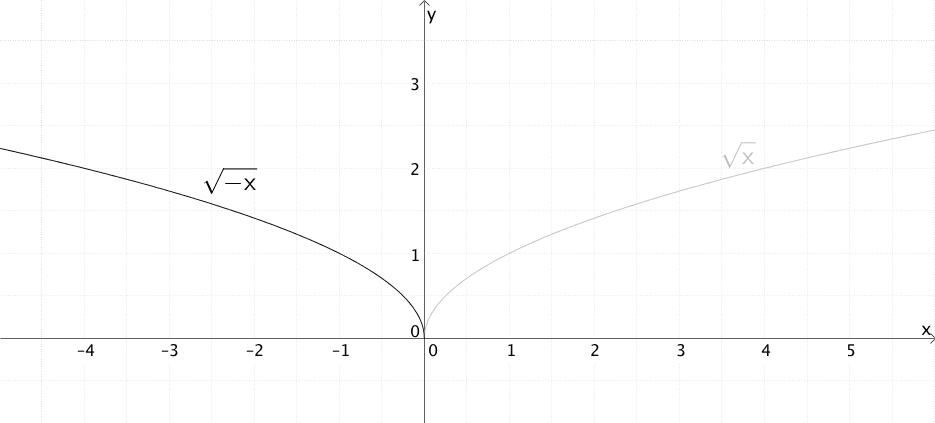
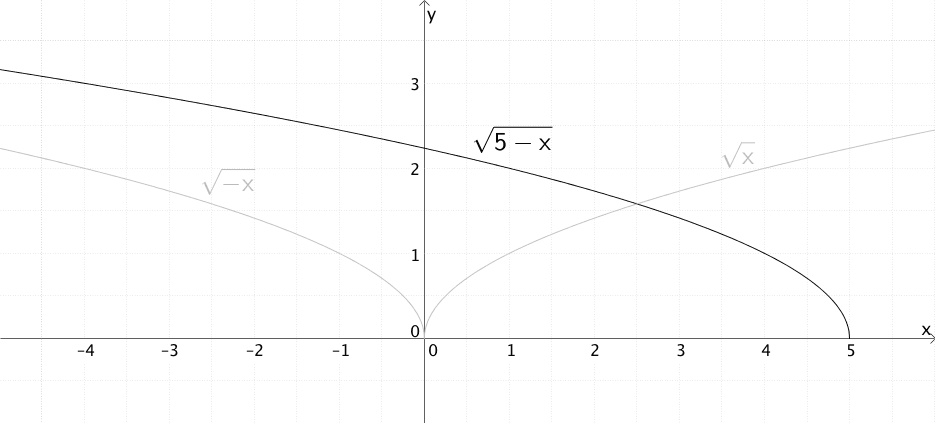
Spiegelt man den Graphen der Funktion \(x \mapsto \sqrt{x}\) mit \(D = \mathbb R_{0}^{+} = [0; +\infty[\) an der \(y\)-Achse, erhalt man den Graphen der Funktion \(x \mapsto \sqrt{-x}\) mit \(D = \mathbb R_{0}^{-} = \; ]-\infty; 0]\). Verschiebt man diesen um 5 in \(x\)-Richtung, entsteht der Graph der Funktion \(x \mapsto \sqrt{5 - x}\) mit \(D = \; ]-\infty; 5]\).
\[x \mapsto \sqrt{x}\,; \enspace D = \mathbb R_{0}^{+} = [0; +\infty[\]
Spiegelung an der \(y\)-Achse:
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[\Longrightarrow \quad x \mapsto \sqrt{-x}\,; \enspace D = \mathbb R_{0}^{-} = \; ]-\infty; 0]\]
Verschiebung um 5 in \(x\)-Richtung:
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\begin{align*} \Longrightarrow \quad x &\mapsto \sqrt{-(x - 5)} \\[0.8em] x &\mapsto \sqrt{5 - x}\,; \enspace D = \; ]-\infty; 5] \end{align*}\]
\[\Longrightarrow \quad g(x) = \sqrt{5 - x}\]
Entstehung des Graphen der Funktion \(x \mapsto \sqrt{5 - x}\) aus dem Graphen der Funktion \(x \mapsto \sqrt{x}\)