Im betrachteten Zeitraum gibt es ein jahr, in dem die Geburtenziffer am stärksten abnimmt. Geben Sie mithilfe von Abbildung 2 einen Näherungswert für dieses Jahr an. Beschreiben Sie, wie man auf der Grundlage des Modells rechnerisch nachweisen könnte, dass die Abnahme der Geburtenziffer von diesem Jahr an kontinuierlich schwächer wird.
(3 BE)
Lösung zu Teilaufgabe 3c
\[g_{1{,}4}(x) = 2x \cdot e^{-0{,}5x^2} + 1{,}4\,; \quad x \geq 0\]
Jahr, in dem die Geburtenziffer am stärksten abnimmt
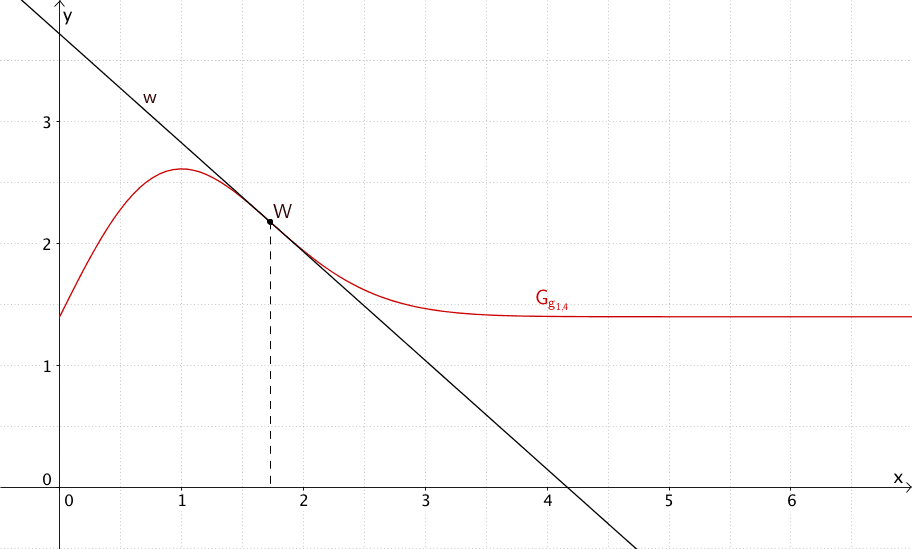
Graph der Funktion \(g_{1{,}4}\) für \(x \geq 0\) mit Wendepunkt \(W\) und Wendetangente \(w\)
Im Intervall \([0;+\infty]\) hat der Graph von \(g_{1{,}4}\) für \(x \approx 1{,}7\) eine Wendestelle an der die momentane Änderungsrate der Geburtenziffer maximal ist. Da \(G_{g_{1{,}4}}\) im Intervall \([1;+\infty]\) zudem strreng monoton fällt, nimmt die Geburtenziffer an der Wendestelle am stärksten ab.
\(x \approx 1{,}7\) entspricht dem Jahr 1972.
Im Jahr 1972 nimmt die Geburtenziffer am stärksten ab.
Beschreibung eines rechnerischen Nachweises dafür, dass die Geburtenziffer ab dem Jahr 1972 kontinuierlich schwächer wird
Vorgehensweise:
1. Nachweis der Wendestelle \(x_W\) von \(G_{g_{1{,}4}}\)
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
2. Nachweis, dass der Graph von \(g_{1{,}4}\) für \(x > x_W\) linksgekrümmt ist.
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
\(g''_{1{,}4}(x) > 0\) für \(x > x_W\)
3. Nachweis, dass die Funktion \(g_{1{,}4}\) für \(x \to \infty\) einen unteren Grenzwert besitzt.
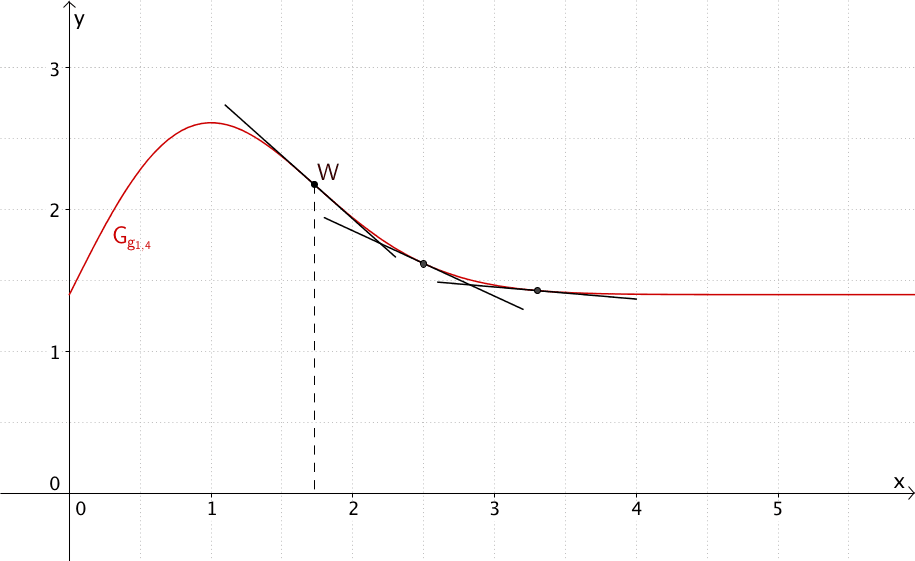
Da der Graph von \(g_{1{,}4}\) für \(x > x_W\) linksgekrümmt ist, nimmt die Steigung einer Tangente an einer Stelle \(x > x_W\) an \(G_{g_{1{,}4}}\) dem Betrag nach ab. Die Tangentensteigung beschreibt die momentane Änderungsrate der Geburtenziffer, also die Abnahme der Geburtenziffer zum Zeitpunkt \(x > x_W\). Somit wird die Abnahme der Geburtenziffer ab dem Zeitpunkt \(x_W\) kontinuierlich schwächer. Der Nachweis des unteren Grenzwerts von \(g_{1{,}4}\) stellt sicher, dass die Geburtenziffer nicht wieder zunimmt, sondern stetig abnimmt.
Ergänzung (nicht Teil der Prüfung!): Rechnerischer Nachweis
Die nachfolgende Ergänzung ist nicht Teil der Prüfung! Sie soll dem besseren Verständnis bzw. der Vertiefung des Themas dienen.
\[g_{1{,}4}(x) = 2x \cdot e^{-0{,}5x^2} + 1{,}4\,; \quad x \geq 0\]
1. Nachweis der Wendestelle \(x_W\) von \(G_{g_{1{,}4}}\)
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
Zweite Ableitung \(g''_{1{,}4}(x)\) bilden:
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[ f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
(vgl. Merkhilfe)
\[\begin{align*} g'_{1{,}4}(x) &= 2 \cdot e^{-0{,}5x^2} + 2x \cdot e^{-0{,}5x^2} \cdot (-0{,}5) \cdot 2x \\[0.8em] &= 2 \cdot e^{-0{,}5x^2} - 2x^2 \cdot e^{-0{,}5x^2} \\[0.8em] &= 2e^{-0{,}5x^2} \cdot (1 - x^2) \end{align*}\]
\[\begin{align*} g''_{1{,}4}(x) &= 2e^{-0{,}5x^2} \cdot (-0{,}5) \cdot 2x \cdot (1 - x^2) + 2e^{-0{,}5x^2} \cdot (-2x) \\[0.8em] &= -2x \cdot e^{-0{,}5x^2} \cdot (1 - x^2) - 4x \cdot e^{-0{,}5x^2} \\[0.8em] &= 2x \cdot e^{-0{,}5x^2} \cdot (x^2 - 3) \end{align*}\]
\[g''_{1{,}4}(x) \overset{!}{=} 0 \quad \Longrightarrow \quad (x = 0) \enspace \vee \enspace x^2 - 3 = 0\]
\[\begin{align*} x^2 - 3 &= 0 & &| + 3 \\[0.8em] x^2 &= 3 & &| \; \sqrt{\quad}\,, \enspace x \geq 0 \\[0.8em] x &= \sqrt{3} \\[0.8em] x &\approx 1{,}73 \end{align*}\]
Vorzeichenwechsel von \(g''_{1{,}4}(x)\) an der Stelle \(x = \sqrt{3}\):
\[g''_{1{,}4}(x) = 2x \cdot e^{-0{,}5x^2} \cdot (x^2 - 3)\]
In der Nähe der Stelle \(x = \sqrt{3}\) gilt für \(x < \sqrt{3}\) und für \(x > \sqrt{3}\):
\[2x \cdot e^{-0{,}5x^2} > 0\]
Somit bestimmt der Falktor \((x^2 - 3)\) den Vorzeichenwechsel von \(g''_{1{,}4}(x)\) an der Stelle \(x = \sqrt{3}\).
Für \(x < \sqrt{3} \quad \Longrightarrow \quad x^2 - 3 < 0 \quad \Longrightarrow \quad g''_{1{,}4}(x) < 0\)
Für \(x > \sqrt{3} \quad \Longrightarrow \quad x^2 - 3 > 0 \quad \Longrightarrow \quad g''_{1{,}4}(x) > 0\)
\(\Longrightarrow \quad x_W = \sqrt{3}\) ist Wendestelle von \(G_{g_{1{,}4}}\).
\(x_W = \sqrt{3} \approx 1{,}73\) entspricht dem Jahr 1972.
2. Nachweis, dass der Graph von \(g_{1{,}4}\) für \(x > x_W\) linksgekrümmt ist.
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
\[x_W = \sqrt{3}\]
\(g''_{1{,}4}(x) > 0\) für \(x > \sqrt{3} \quad \Longrightarrow \quad G_{g_{1{,}4}}\) ist linksgekrümmt.
3. Nachweis, dass die Funktion \(g_{1{,}4}\) für \(x \to \infty\) einen unteren Grenzwert besitzt.
Verhalten von \(g_{1{,}4}(x)\) für \(x \to + \infty\):
Wichtiger Grenzwert
\[\lim \limits_{x \, \to \, +\infty} \frac{x^r}{e^x} = 0 \enspace (r > 0)\]
Für \(\,x \to +\infty\,\) wächst \(e^x\) „schneller" als jede Potenz \(x^r \enspace (r > 0)\).
(vgl. Merkhilfe)
\[\begin{align*} \lim \limits_{x \, \to \, + \infty} g_{1{,}4}(x) &= \lim \limits_{x \, \to \, + \infty} 2x \cdot e^{-0{,}5x^2} + 1{,}4 \\[0.8em] &= \lim \limits_{x \, \to \, + \infty} \; \frac{2x}{e^{0{,}5x^2}} + 1{,}4 \\[0.8em] &= 1{,}4 \end{align*}\]
Für \(x \to + \infty\) wächst \(e^{0{,}5x^2}\) schneller als \(x\).
Fazit:
Ab dem Jahr 1972 wird die Abnahme der Geburtenziffer kontinuierlich schwächer und nähert sich dem unteren Grenzwert 1,4.


