Der Graph \(G_f\) besitzt in genau einem Punkt eine waagrechte Tangente. Bestimmen Sie die Koordinaten dieses Punkts und begründen Sie, dass es sich um einen Hochpunkt handelt.
(zur Kontrolle: \(f'(x) = \dfrac{10 - 2x}{\sqrt{10x - x^2}}\); \(y\)-Koordinate des Hochpunkts: \(10\))
(5 BE)
Lösung zu Teilaufgabe b
\[f(x) = 2 \cdot \sqrt{10x - x^2}; \; D_{f} = [0;10]\]
Bestimmung der Koordinaten des Punkts, in dem \(G_f\) eine waagrechte Tangente besitzt
Die Bedingung für eine waagrechte Tangente (Steigung ist null) von \(G_{f}\) lautet:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[f'(x) = 0\]
Erste Ableitung \(f'\) bilden:
Hierfür wird entweder u. a. die Kettenregel sowie die Ableitung einer Wurzelfunktion benötigt, oder man formuliert den Wurzelterm in der Potenzschreibweise und verwendet die Ableitung einer Potenzfunktion.
\[\begin{align*}f(x) &= 2 \cdot \sqrt{10x - x^2} &&| \; \sqrt{a} = a^{\frac{1}{2}} \; \left(\text{allg.:}\; \sqrt[n]{a^m} = a^{\frac{m}{n}}\right) \\[0.8em] &= 2 \cdot (10x - x^2)^{\frac{1}{2}}\end{align*}\]
1. Möglichkeit: Wurzelfunktion ableiten
\[f(x) = 2 \cdot \textcolor{#0087c1}{\sqrt{\textcolor{#cc071e}{10x - x^2}}}; \; D_{f} = [0;10]\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[f'(x) = 2 \cdot \underbrace{\textcolor{#0087c1}{\frac{1}{2\sqrt{\textcolor{#cc071e}{10x - x^2}}}} \cdot \textcolor{#cc071e}{(10 - 2x)}}_{\text{Kettenregel}} = \frac{10 - 2x}{\sqrt{10x - x^2}}\]
2. Möglichkeit: Potenzfunktion ableiten
\[f(x) = 2 \cdot \textcolor{#0087c1}{(\textcolor{#cc071e}{10x - x^2})^{\frac{1}{2}}}; \; D_{f} = [0;10]\]
\[\begin{align*}f'(x) &= 2 \cdot \underbrace{\textcolor{#0087c1}{\frac{1}{2} \cdot (\textcolor{#cc071e}{10x - x^2})^{-\frac{1}{2}}} \cdot \textcolor{#cc071e}{(10 - 2x)}}_{\text{Kettenregel}} &&| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= \frac{10 - 2x}{(10x - x^2)^{\frac{1}{2}}} &&| \; a^{\frac{1}{2}} = \sqrt{a} \\[0.8em] &= \frac{10 - 2x}{\sqrt{10x - x^2}}\end{align*}\]
Nullstelle von \(f'\) bestimmen:
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\[f'(x) = \frac{\textcolor{#e9b509}{10 - 2x}}{\sqrt{10x - x^2}}\]
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
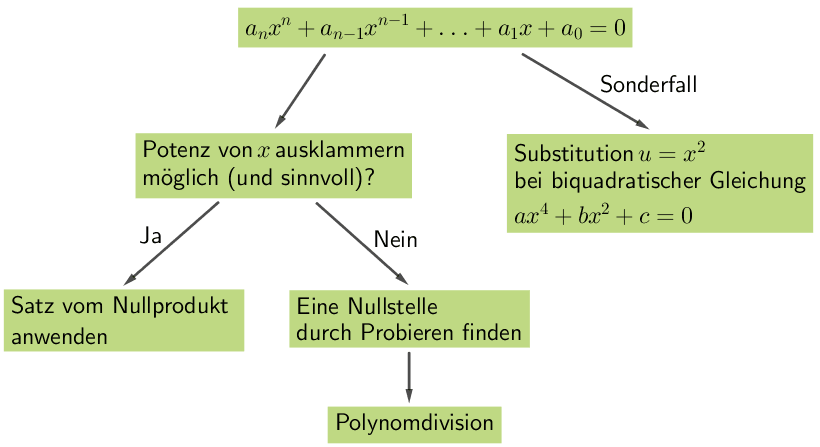
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
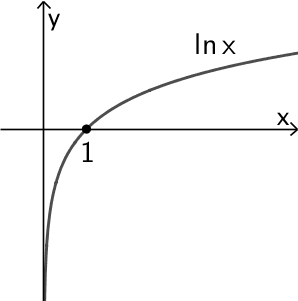
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
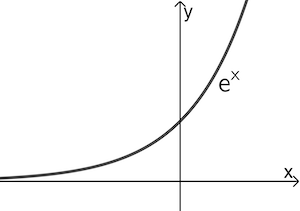
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[\begin{align*}f'(x) = 0 \enspace \Rightarrow \enspace \textcolor{#e9b509}{10 - 2x} &\textcolor{#e9b509}{=} \textcolor{#e9b509}{0} &&| + 2x \\[0.8em] 10 &= 2x &&| : 2 \\[0.8em] 5 &= x\end{align*}\]
\[f(5) = 2 \cdot \sqrt{10 \cdot 5 - 5^2} = 2 \cdot \sqrt{25} = 2 \cdot 5 = 10\]
Somit besitzt \(G_f\) in genau dem einen Punkt \((5|10)\) eine waagrechte Tangente.
Begründung, dass der Punkt \((5|10)\) ein Hochpunkt von \(G_f\) ist
Die Begründung kann im einfachsten Fall mithilfe des Wertebereichs von \(f\) erfolgen, aber auch durch den Nachweis eines entsprechenden Vorzeichenwechsels von \(f'\) mit einer Monotonietabelle oder auf halbgrafischem Weg.
1. Möglichkeit: Wertebereich von \(f\) betrachten
\[f(x) = 2 \cdot \textcolor{#e9b509}{\underbrace{\sqrt{10x - x^2}}_{\geq \,0}}; \; D_f = [0;10]\]
Es gilt: \(\textcolor{#e9b509}{f(x) \geq 0}\) für alle \(x \in D_f\). Mit \(f(0) = 0\), \(f(10) = 0\) (vgl. Teilaufgabe a) und \(f(5) = 10\) ist der Punkt \((5|10)\) ein Hochpunkt von \(G_f\).
2. Möglichkeit: Monotonietabelle
Der Punkt \((5|10)\) ist ein Hochpunkt von \(G_f\), wenn \(f'\) an der Stelle \(x = 5\) einen Vorzeichenwechsel von \(\textcolor{#0087c1}{\boldsymbol{+}}\) nach \(\textcolor{#cc071e}{\boldsymbol{-}}\) hat. Denn dann wechselt \(G_f\) an der Stelle \(x = 5\) das Monotonieverhalten von streng monoton steigend zu streng monoton fallend.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[f'(x) = \frac{10 - 2x}{\sqrt{10x - x^2}} = \frac{2 \cdot \textcolor{#89ba17}{(5 - x)}}{\textcolor{#e9b509}{\underbrace{\sqrt{10x - x^2}}_{> \, 0 \; \text{für}\,x\,\in\;]0;10[}}}\]
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
Der Zählerterm \(\textcolor{#89ba17}{(5 - x)}\) von \(f'(x)\) bestimmt den Vorzeichnewechsel von \(f'\) an der Stelle \(x = 5\).
| \(x\) | \(]0;5[\) | \(5\) | \(]5;10[\) |
| \(\textcolor{#89ba17}{(5 - x)}\) | \(\textcolor{#0087c1}{\boldsymbol{+}}\) | \(0\) | \(\textcolor{#cc071e}{\boldsymbol{-}}\) |
| \(f'(x)\) | \(\textcolor{#0087c1}{\boldsymbol{+}}\) | \(0\) | \(\textcolor{#cc071e}{\boldsymbol{-}}\) |
| \(G_f\) | \(\textcolor{#0087c1}{\nearrow}\) | \(HoP\) | \(\textcolor{#cc071e}{\searrow}\) |
Oder geeignete Funktionswerte berechnen, beispielsweise \(f'(4) = \dfrac{2}{\sqrt{24}} \textcolor{#0087c1}{> 0}\) und \(f'(6) = -\dfrac{2}{\sqrt{24}} \textcolor{#cc071e}{< 0}\).
Also ist der Punkt \((5|10)\) ein Hochpunkt von \(G_f\).
3. Möglichkeit: halbgrafischer Nachweis des Vorzeichenwechsels von \(f'\)
\[f'(x) = \frac{\textcolor{#89ba17}{(10 - 2x)}}{\textcolor{#e9b509}{\underbrace{\sqrt{10x - x^2}}_{> \, 0 \; \text{für}\,x\,\in\;]0;10[}}}\]
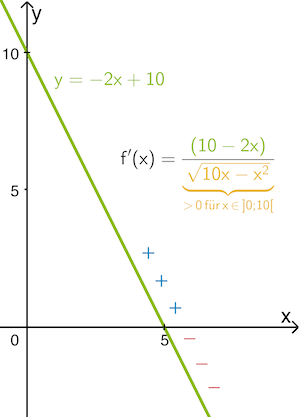
Der lineare Zählerterm \(\textcolor{#89ba17}{10 - 2x}\) bestimmt den Vorzeichenwechsel von \(f'\). Dieser kann durch die Gerade mit der Gleichung \(\textcolor{#89ba17}{y = -2x + 10}\) veranschaulicht werden. Es genügt eine qualitative Skizze unter Berücksichtigung der Punkte \((0|10)\) (\(y\)-Achsenabschnitt) und \((5|0)\) (vgl. Nullstelle \(x = 5\) von \(f'\)).
Da die Gerade an der Nullstelle \(x = 5\) von \(\textcolor{#0087c1}{\boldsymbol{+}}\) nach \(\textcolor{#cc071e}{\boldsymbol{-}}\) verläuft, hat \(\boldsymbol{f'}\) dort einen Vorzeichenwechsel von \(\textcolor{#0087c1}{\boldsymbol{+}}\) nach \(\textcolor{#cc071e}{\boldsymbol{-}}\).
Folglich ist der Punkt \((5|10)\) ein Hochpunkt von \(G_f\).


