Laplace-Experiment
Ein Zufallsexperiment bei dem alle Ergebnisse \(\omega_{i}\) aus dem Ergebnisraum \(\Omega = \{\omega_{1}, \omega_{2}, ..., \omega_{k}\}\) (alle möglichen Versuchsausgänge) gleichwahrscheinlich sind, heißt Laplace-Experiment. Ist diese Voraussetzung erfüllt, kann die Wahrscheinlichkeit eines Ereignisses \(A\) mithilfe der Formel von Laplace (Pierre Simon Laplace) berechnet werden. Typische Laplace-Experimente sind das Werfen eines homogenen Würfels (Laplace-Würfel), das Werfen einer homogenen Münze (Laplace-Münze) oder das Drehen eines Glücksrads mit gleich großen Sektoren.
Laplace-Wahrscheinlichkeit
\[P(A) = \frac{\vert A \vert}{\vert \Omega \vert} = \frac{\text{Anzahl der für}\; A \; \text{günstigen Ergebnisse}}{\text{Anzahl der insgesamt möglichen Ergebnisse}}\]
Beispielaufgabe
Ein Glücksrad, dessen zwölf gleich große Sektoren mit den Zahlen 1 bis 12 beschriftet sind, wird einmal gedreht (vgl. Abbildung). Es wird die Zahl betrachtet, auf die der Pfeil zeigt, nachdem das Glücksrad zum Stillstand gekommen ist.
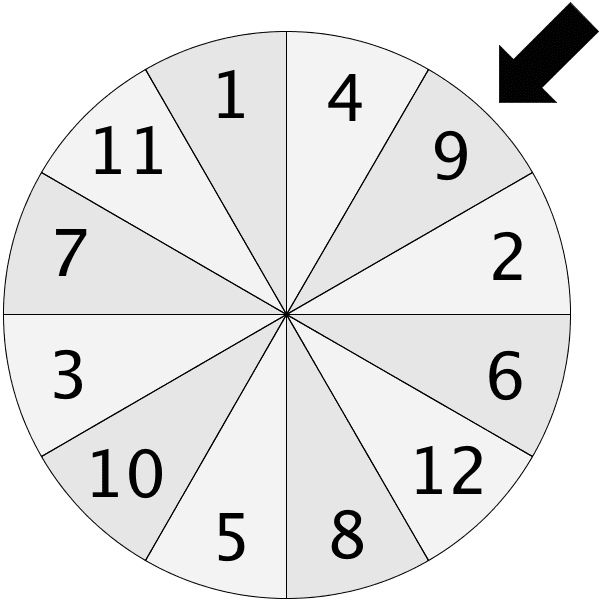
Berechnen Sie die Wahrscheinlichkeit für folgende Ereignisse:
\(A\): „Die Zahl ist eine gerade Zahl."
\(B\): „Die Zahl ist eine durch drei ganzzahlig teilbare Zahl."
\(C\): „Die Zahl ist eine Primzahl."
Ergebnisraum \(\Omega\):
\[\Omega = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}\]
Da die Sektoren des Glücksrads gleich groß sind, ist das Eintreten von jedem der 12 möglichen Ergebnisse gleichwahrscheinlich. Folglich liegt ein Laplace-Experiment vor.
\[\Longrightarrow \quad P(\{1\}) = P(\{2\}) = \dots = P(\{12\}) = \frac{1}{12}\]
Mächtigkeit \(\vert \Omega \vert\) des Ergebnisraums \(\Omega\):
Die Anzahl der möglichen Ergebnisse des Ergebnisraums \(\Omega\) ist zwölf.
\[\vert \Omega \vert = 12\]
Wahrscheinlichkeit des Ereignisses \(A\)
\(A\): „Die Zahl ist eine gerade Zahl."
\[A = \{2,4,6,8,10,12\}\]
Das Ereignisses \(A\) zählt sechs Elemente.
\[\vert A \vert = 6\]
\[P(A) = \frac{\vert A \vert}{\vert \Omega \vert} = \frac{6}{12} = \frac{1}{2}\]
Wahrscheinlichkeit des Ereignisses \(B\)
\(B\): „Die Zahl ist eine durch drei ganzzahlig teilbare Zahl."
\[B = \{3,6,9,12\}\]
Das Ereignisses \(B\) zählt vier Elemente.
\[\vert B \vert = 4\]
\[P(B) = \frac{\vert B \vert}{\vert \Omega \vert} = \frac{4}{12} = \frac{1}{3}\]
Wahrscheinlichkeit des Ereignisses \(C\)
\(C\): „Die Zahl ist eine Primzahl."
\[C = \{2,3,5,7,11\}\]
Das Ereignisses \(C\) zählt fünf Elemente.
\[\vert C \vert = 5\]
\[P(C) = \frac{\vert C \vert}{\vert \Omega \vert} = \frac{5}{12}\]

