Die zunächst leere Dose wird langsam mit Flüssigkeit gefüllt, bis die maximale Füllhöhe von 15 cm erreicht ist. Beschreiben Sie mithilfe von Abbildung 2 die Bewegung des Schwerpunkts \(S\) während des Füllvorgangs. Welche Bedeutung im Sachzusammenhang hat die Tatsache, dass \(x\)-Koordinate und \(y\)-Koordinate des Tiefpunkts von \(G_f\) übereinstimmen?

(3 BE)

Lösung zu Teilaufgabe 3b

\[f(x) = \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\,; \quad 0 \leq x \leq 15\]

Beschreibung der Bewegung des Schwerpunkts \(S\) während des Füllvorgangs

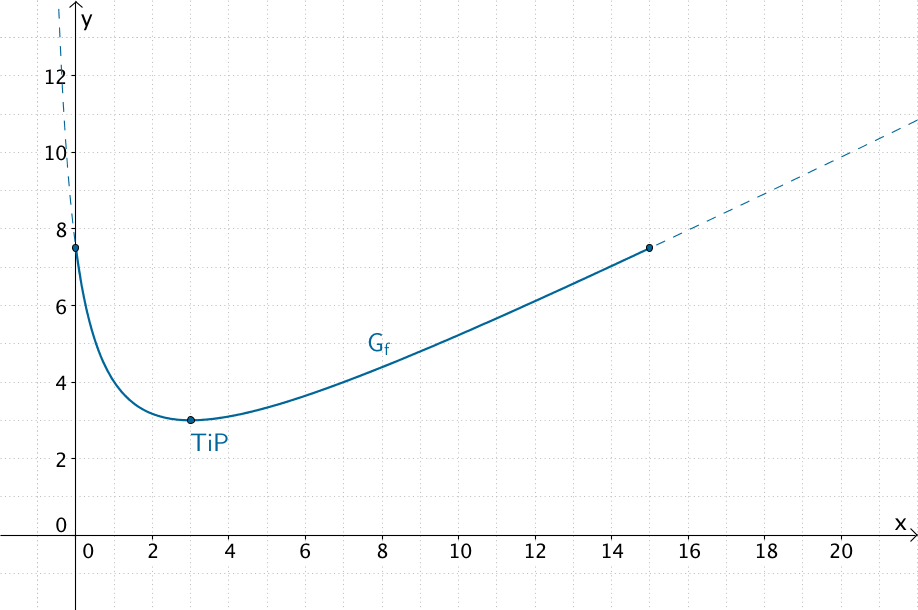
Bei der leeren Dose beträgt die Höhe des Schwerpunkts \(S\) über dem Dosenboden 7,5 cm (siehe Teilaufgabe 3a).

Wird die zunächst leere Dose langsam mit Flüssigkeit gefüllt, nimmt die Höhe des Schwerpunkts \(S\) für \(0 < x <3\) kontinuierlich ab. Bei einer Füllhöhe von 3 cm \((x = 3)\) ist die Höhe des Schwerpunkts \(S\) über dem Dosenboden mit ebenfalls 3 cm \((f(3) = 3)\) minimal.

Wird die Dose weiter mit Flüssigkeit gefüllt, nimmt die Höhe des Schwerpunkts \(S\) für \(3 < x < 15\) kontinuierlich zu, bis diese bei vollständiger Füllung wieder 7,5 cm beträgt.

Bedeutung des Tiefpunkts von \(G_f\) im Sachzusammenhang

Wenn die Füllhöhe 3 cm beträgt, befindet sich der Schwerpunkt \(S\) mit ebenfalls 3 cm in seiner geringsten Höhe \((TiP\,(3|3))\). Der Schwerpunkt liegt dann auf der Flüssigkeitsoberfläche.