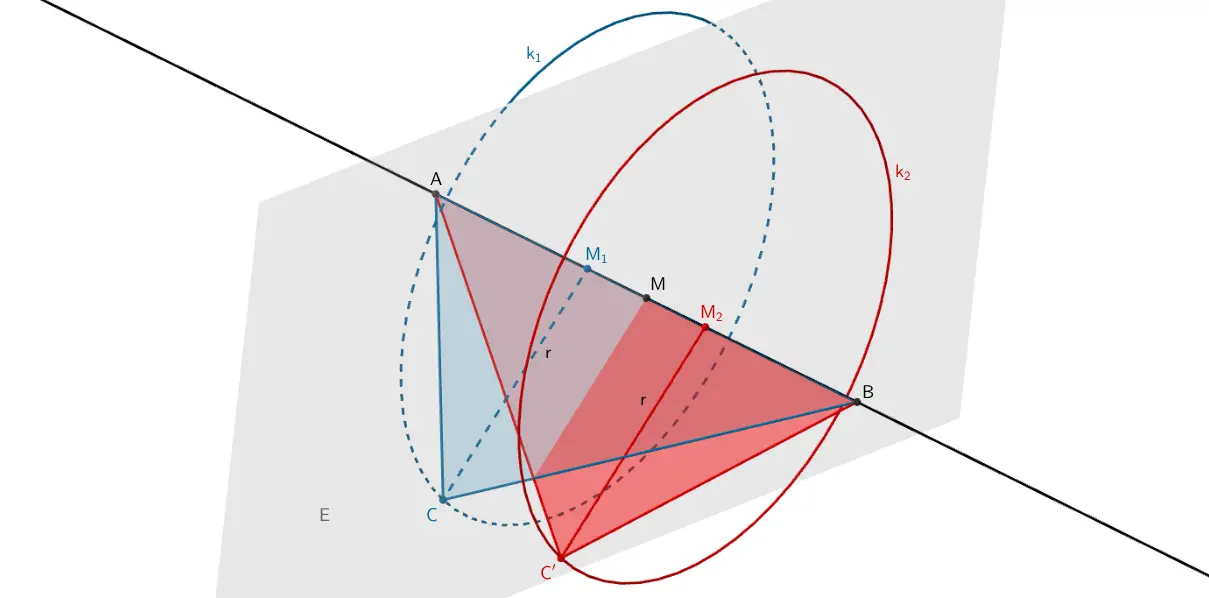
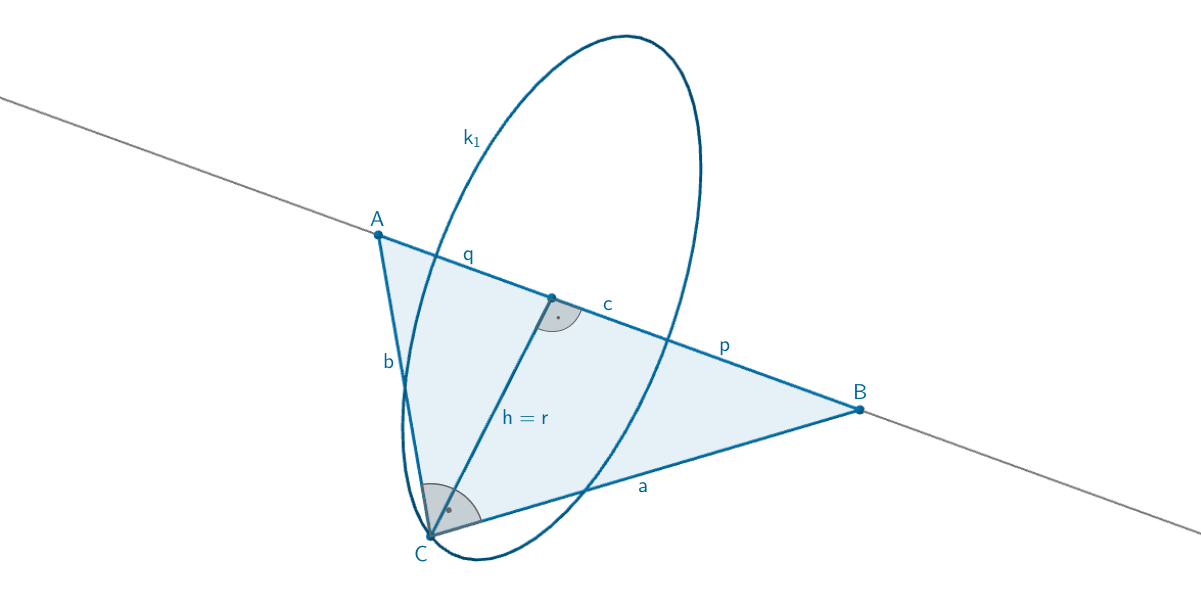
Alle Punkte \(C^\ast\) im Raum, die zusammen mit \(A\) und \(B\) ein zum Dreieck \(ABC\) kongruentes Dreieck festlegen, bilden zwei gleich große Kreise. Beschreiben Sie (z.B. durch eine Skizze) die Lage der beiden Kreise bezüglich der Strecke \([AB]\) und ermitteln Sie den Radius der beiden Kreise.
(6 BE)
Lösung zu Teilaufgabe b
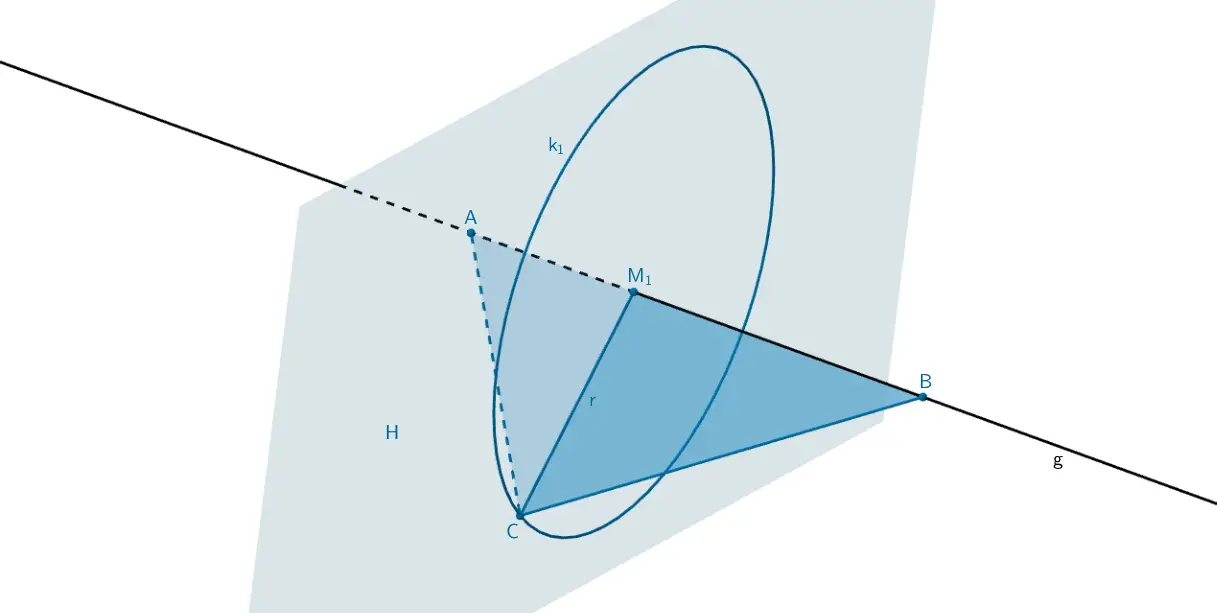
1. Lösungsansatz mit Hilfsebene
2. Lösungsansatz: Anwenden des Skalarprodukts
3. Lösungsansatz: Anwenden der Differentialrechnung
4. Lösungsansatz: Höhen- und Kathetensatz im rechtwinkligen Dreieck \(ABC\) anweden
5. Lösungsansatz: Fläche des rechtwinkligen Dreiecks \(ABC\) bestimmen
Die Punkte \(C^\ast\) liegen einerseits auf einem Kreis \(k_1\), der durch Rotation des Punktes \(C\) um die Gerade \(AB\) festgelegt wird. Die Länge des Radius \(r\) des Kreises \(k_1\) ist gleich dem Abstand des Punktes \(C\) von der Geraden \(AB\). Durch Spiegelung des Punktes \(C\) an einer Ebene \(E\), die den Mittelpunkt \(M\) der Strecke \([AB]\) enthält und auf der Geraden \(AB\) senkrecht ist, entsteht der Bildpunkt \(C^{\,\prime}\). Weitere Punkte \(C^\ast\) liegen auf einem Kreis \(k_2\), der durch Rotation des Punktes \(C^{\,\prime}\) um die Gerade \(AB\) festgelegt wird. Die Länge des Radius \(r\) des Kreises \(k_2\) ist gleich dem Abstand des Punktes \(C^{\,\prime}\) von der Geraden \(AB\).
Es sei \(g\) die Gerade durch die Punkte \(A\) und \(B\).
\[r = d(C, g) = d(C, M_1) = d(C', M_2)\]
1. Lösungsansatz mit Hilfsebene
Abstand Punkt - Gerade, Ansatz: Hilfsebene aufstellen
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
1. Hilfsebene \(H\) mit den Eigenschaften \(P \in H\) und \(H \perp g\) bestimmen:
\[H \colon \overrightarrow{n}_H \circ \left( \overrightarrow X - \overrightarrow P \right) = 0\,; \quad \overrightarrow{n}_H = \overrightarrow u\]
2. Schnittpunkt \(S\) der Ebene \(H\) mit der Geraden \(g\) ermitteln:
\(H \cap g \colon \overrightarrow{n}_H \circ \left( \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \right) = 0 \quad \Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[S \in g \colon \overrightarrow S = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([PS]\) berechnen:
\[d\,(P; g) = \overline{PS} = \vert \overrightarrow P - \overrightarrow S \vert\]
Die Hilfsebene \(H\) mit den Eigenschaften \(C \in H\) und \(H \perp g\) schneidet die Gerade \(g\) im Punkt \(M_1\).
Gleichung der Geraden \(g\) aufstellen:
\[A\,(1|7|3)\,, \qquad B\,(6|-7|1)\]
\[g \colon \enspace \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow{AB}\,, \quad \lambda \in \mathbb R\]
\[\overrightarrow{AB} = \overrightarrow B - \overrightarrow A = \begin {pmatrix} 6 \\ -7 \\ 1 \end {pmatrix} - \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} = \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix}\]
\[g \colon \enspace \overrightarrow X = \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix}\]
Hilfsebene \(H\) mit den Eigenschaften \(C \in H\) und \(H \perp g\) bestimmen:
\[C\,(-2|1|-3)\]
\[\overrightarrow {n}_F = \overrightarrow {u}_g = \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix}\]
\[H \colon \enspace \overrightarrow{n}_H \circ \left( \overrightarrow X - \overrightarrow C \right) = 0\]
\[H \colon \; \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} -2 \\ 1 \\ -3 \end {pmatrix} \right] = 0\]
Schnittpunkt \(M_1\) der Ebene \(H\) mit der Geraden \(g\) ermitteln:
Zur Berechnung des Schnittpunktes \(M_1\) setzt man den Ortsvektor \(\overrightarrow X\) aus der Gleichung von \(g\) in die Normalengleichung der Hilfsebene \(H\) ein und löst die Gleichung nach dem Parameter \(\lambda\) auf.
\[g \colon \enspace \overrightarrow X = \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix}\]
\[H \colon \; \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} -2 \\ 1 \\ -3 \end {pmatrix} \right] = 0\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin {align*} g \cap H \colon \enspace \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix} \circ \left[ \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix} - \begin {pmatrix} -2 \\ 1 \\ -3 \end {pmatrix} \right] &= 0 \\[0.8em] \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix} \circ \left[ \begin {pmatrix} 3 \\ 6 \\ 6 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix} \right] &= 0 \\[0.8em] 5 \cdot (3 + 5 \lambda) - 14 \cdot\ (6 - 14 \lambda) - 2 \cdot (6 - 2 \lambda) &= 0 \\[0.8em] 15 + 25 \lambda - 84 + 196 \lambda -12 + 4 \lambda &= 0 \\[0.8em] -81 + 225 \lambda &= 0 \\[0.8em] \lambda &= \frac{9}{25}\end {align*}\]
Parameterwert \(\lambda = \frac{9}{25}\) in \(g\) einsetzen:
\[M_1 \in g \colon \enspace \overrightarrow {M}_1 = \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} + \frac{9}{25} \cdot \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix} = \begin {pmatrix} \frac{14}{5} \\ \frac{49}{25} \\ \frac{57}{25} \end {pmatrix}\]
Länge der Strecke \([CM_1]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}\overline{CM_1} &= \left| \overrightarrow {M}_1 - \overrightarrow C \right| \\[0.8em] &= \left| \begin {pmatrix} \frac{14}{5} \\ \frac{49}{25} \\ \frac{57}{25} \end {pmatrix} - \begin {pmatrix} -2 \\ 1 \\ -3 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} \frac{24}{5} \\ \frac{24}{25} \\ \frac{132}{25} \end {pmatrix} \right| \\[0.8em] &= \sqrt{\left(\frac{24}{5}\right)^2 + \left(\frac{24}{25}\right)^2 + \left(\frac{132}{25}\right)^2} \\[0.8em] &= \frac{36}{5} \\[0.8em] &= 7{,}2 \end{align*}\]
\[\Longrightarrow \quad r = 7{,}2\]
Der Radius der beiden Kreise, deren Punkte \(C^\ast\) zusammen mit den Punkten \(A\) und \(B\) kongruente Dreiecke \(ABC^\ast\) festlegen, beträgt \(7{,}2\) LE (Längeneinheiten).
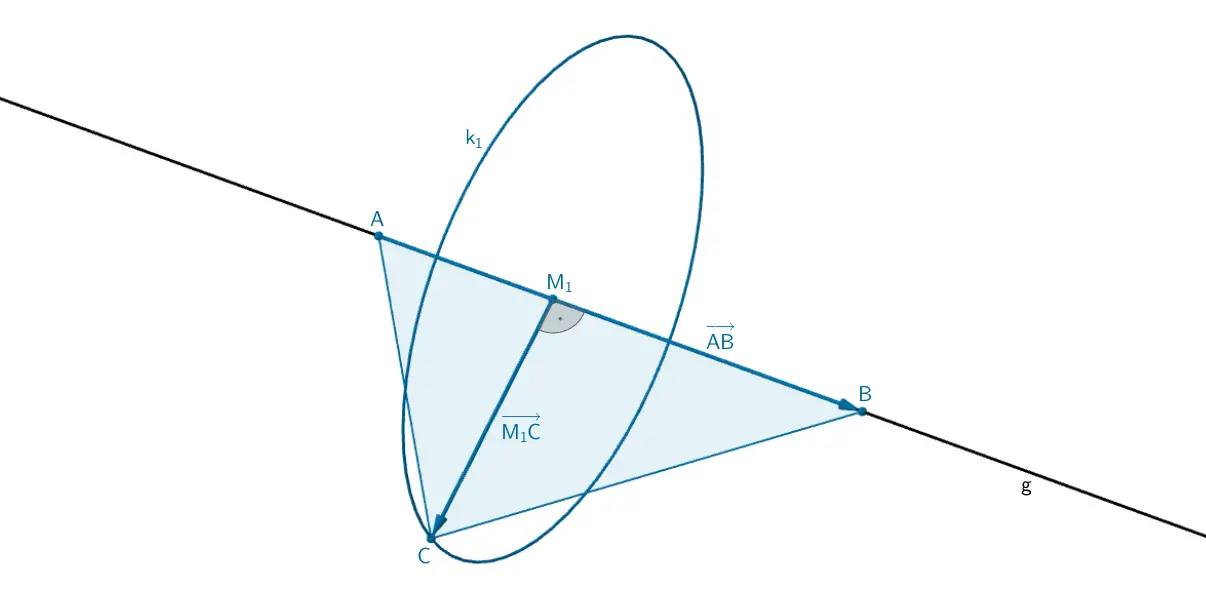
2. Lösungsansatz: Anwenden des Skalarprodukts
\[C\,(-2|1|-3)\,, \qquad g \colon \enspace \overrightarrow X = \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix}\,, \quad \lambda \in \mathbb R\]
Abstand Punkt - Gerade, Ansatz: Skalarprodukt anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(P\) auf die Gerade \(g\).
Somit gilt: \(\enspace \overrightarrow{FP} \perp \overrightarrow{u} \quad \Longleftrightarrow \quad \overrightarrow{FP} \circ \overrightarrow{u} = 0\)
1. Verbindungsvektor \(\overrightarrow{FP}\) allgemein beschreiben:
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u \quad \Longrightarrow \quad \overrightarrow{FP} = \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \]
2. Koordinaten des Lotfußpunktes \(F\) bestimmen:
\[\overrightarrow{FP} \circ \overrightarrow{u} = 0 \quad \Longleftrightarrow \quad \left[ \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \right] \circ \overrightarrow u = 0\]
\(\Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([FP]\) berechnen:
\[d\,(P;g) = \overline{FP} = \vert \overrightarrow P - \overrightarrow F \vert\]
Der Mittelpunkt \(M_1\) des Kreises \(k_1\) ist der Lotfußpunkt des Lotes des Punktes \(C\) auf die Gerade \(g\).
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
Somit gilt: \(\overrightarrow{M_1C} \perp \overrightarrow{AB} \quad \Longleftrightarrow \quad \overrightarrow{M_1C} \circ \overrightarrow{AB} = 0\)
Vektor \(\overrightarrow{M_1C}\) allgemein beschreiben:
\[M_1 \in g \colon \enspace \overrightarrow{M}_1 = \begin{pmatrix} 1 + 5 \lambda \\ 7 - 14 \lambda \\ 3 - 2 \lambda \end{pmatrix}\]
\[\begin{align*} \overrightarrow{M_1C} &= \overrightarrow C - \overrightarrow{M}_1 \\[0.8em] &= \begin{pmatrix} -2 \\ 1 \\ -3 \end{pmatrix} - \begin{pmatrix} 1 + 5 \lambda \\ 7 - 14 \lambda \\ 3 - 2 \lambda \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -3 - 5 \lambda \\ -6 + 14 \lambda \\ -6 + 2 \lambda \end{pmatrix} \end{align*}\]
Koordinaten des Kreismittelpunktes \(M_1\) bestimmen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{M_1C} \circ \overrightarrow{AB} &= 0 \\[0.8em] \begin{pmatrix} -3 - 5 \lambda \\ -6 + 14 \lambda \\ -6 + 2 \lambda \end{pmatrix} \circ \begin{pmatrix} 5 \\ -14 \\ -2 \end{pmatrix} &= 0 \\[0.8em] (-3 - 5 \lambda) \cdot 5 + (-6 + 14 \lambda) \cdot (-14) + (-6 + 2 \lambda) \cdot (-2) &= 0 \\[0.8em] -15 - 25 \lambda +84 - 196 \lambda + 12 - 4 \lambda &= 0 \\[0.8em] 81 - 225 \lambda &= 0 \\[0.8em] -225 \lambda &= -81 \\[0.8em] \lambda &= \frac{9}{25} \end{align*}\]
Parameterwert \(\lambda = \frac{9}{25}\) in \(g\) einsetzen:
\[M_1 \in g \colon \enspace \overrightarrow {M}_1 = \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} + \frac{9}{25} \cdot \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix} = \begin {pmatrix} \frac{14}{5} \\ \frac{49}{25} \\ \frac{57}{25} \end {pmatrix}\]
Länge der Strecke \([CM_1]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}\overline{CM_1} &= \left| \overrightarrow {M}_1 - \overrightarrow C \right| \\[0.8em] &= \left| \begin {pmatrix} \frac{14}{5} \\ \frac{49}{25} \\ \frac{57}{25} \end {pmatrix} - \begin {pmatrix} -2 \\ 1 \\ -3 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} \frac{24}{5} \\ \frac{24}{25} \\ \frac{132}{25} \end {pmatrix} \right| \\[0.8em] &= \sqrt{\left(\frac{24}{5}\right)^2 + \left(\frac{24}{25}\right)^2 + \left(\frac{132}{25}\right)^2} \\[0.8em] &= \frac{36}{5} \\[0.8em] &= 7{,}2 \end{align*}\]
\[\Longrightarrow \quad r = 7{,}2\]
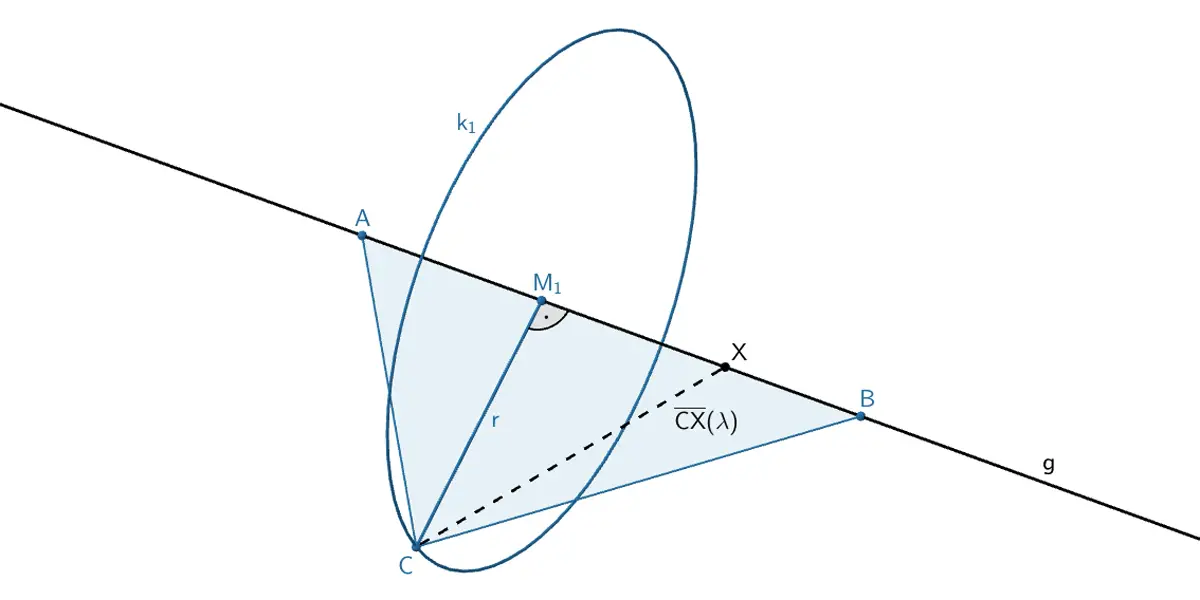
3. Lösungsansatz: Anwenden der Differentialrechnung
\[C\,(-2|1|-3)\,, \qquad g \colon \enspace \overrightarrow X = \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix}\,, \quad \lambda \in \mathbb R\]
Abstand Punkt - Gerade, Ansatz: Differentialrechnung anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
1. Länge der Strecke \([PX]\) zwischen dem Punkt \(P\) und einem beliebigen Punkt \(X \in g\) beschreiben:
\[\overline{PX} = \vert \overrightarrow X - \overrightarrow P \vert \quad \Longrightarrow \quad \overline{PX}(\lambda) = \vert \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \vert\]
2. Parameterwert \(\lambda_{min}\) für minimale Länge bestimmen:
\[\left. \begin{align*} &\overline{PX}^{\;\prime}(\lambda_{min}) \enspace = \enspace 0 \\ \\ &\overline{PX}^{\;\prime \prime}(\lambda_{min}) \; > \enspace 0 \end{align*} \right\} \quad \Longrightarrow \quad \lambda_{min} \]
3. Minimale Länge berechnen:
\[\overline{PX}(\lambda_{min}) = d\,(P;g)\]
Die Länge der Strecke \(\,[CX]\,\) zwischen dem Punkt \(\,C\,\) und einem beliebeigne Punkt \(\,X \in g\,\) lässt sich in Abhängigkeit des Parameterwertes \(\,\lambda\,\) der Geradengleichung von \(\,g\,\) beschreiben.
Länge der Strecke \([CX]\) in Abhängigkeit von \(\lambda\,\):
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{CX} = \vert \overrightarrow X - \overrightarrow C \vert\]
\[\begin{align*} \overline{CX}(\lambda) &= \left| \begin{pmatrix} 1 + 5 \lambda \\ 7 - 14 \lambda \\ 3 - 2 \lambda \end{pmatrix} - \begin{pmatrix} -2 \\ 1 \\ -3 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 3 + 5 \lambda \\ 6 - 14 \lambda \\ 6 - 2 \lambda \end{pmatrix} \right| \\[0.8em] &= \sqrt{(3 + 5 \lambda)^2 + (6 - 14 \lambda)^2 + (6 - 2 \lambda)^2} \\[0.8em] &= \sqrt{9 + 30 \lambda + 25 \lambda^2 + 36 - 168 \lambda + 196 \lambda^2 + 36 - 24 \lambda + 4 \lambda^2} \\[0.8em] &= \sqrt{225 \lambda^2 -162 \lambda + 81} \\[0.8em] &= \sqrt{9\left( 25 \lambda^2 -18 \lambda + 9 \right)} \\[0.8em] &= 3 \sqrt{25 \lambda^2 - 18 \lambda +9} \end{align*}\]
Parameterwert \(\lambda_{min}\) für minimale Länge bestimmen:
\(\overline{CX}(\lambda)\) ist minimal, wenn der Wert des Radikanden minimal ist.
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
\[\left[ 25 \lambda^2 - 18 \lambda + 9 \right]' \enspace \overset{!}{=} \enspace 0\]
Erste Ableitung des Radikanden bilden:
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\left[ 25 \lambda^2 -18 \lambda + 9 \right]' = 50 \lambda - 18\]
\[\begin{align*} \Longrightarrow \quad 50 \lambda - 18 &= 0 \\[0.8em] 50 \lambda &= 18 \\[0.8em] \lambda &=\frac{9}{25} \end{align*}\]
Art der Extremstelle:
\[\left[ 25 \lambda^2 - 18 \lambda + 9 \right]'' = \left[ 50 \lambda - 18 \right]' = 50\]
\[\Longrightarrow \quad \left[ 25 \lambda^2 - 18 \lambda + 9 \right]'' > 0\]
\(\Longrightarrow \quad \overline{CX}(\lambda)\) ist für \(\lambda_{min} = \frac{9}{25}\) minimal.
Minimale Länge berechnen:
\[\begin{align*} \overline{CX}(\lambda_{min}) &= 3 \sqrt{25 \cdot \left( \frac{9}{25} \right)^2 - 18 \cdot \left( \frac{9}{25} \right) + 9} \\[0.8em] &= 3 \sqrt{\frac{81}{25} - \frac{162}{25} + \frac{225}{25}} \\[0.8em] &= 3 \sqrt{\frac{144}{25}} \\[0.8em] &= 3 \cdot \frac{12}{5} \\[0.8em] &= 7{,}2 \end{align*}\]
\[\Longrightarrow \quad r = 7{,}2\]
4. Lösungsansatz: Höhen- und Kathetensatz im rechtwinkligen Dreieck \(ABC\) anwenden
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
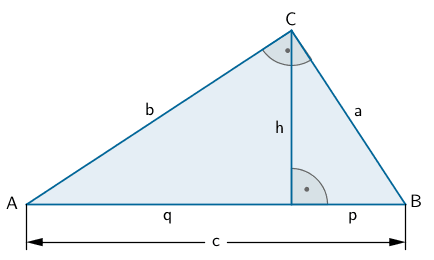
Die Höhe \(h\) des rechtwinkligen Dreiecks \(ABC\) entspricht dem Radius \(r\) der beiden Kreise, die im Raum die Menge aller Punkte \(C^\ast\) der kongruenten Dreiecke \(ABC^\ast\) festlegen.
Mit \(A\,(1|7|3), \enspace B\,(6|-7|1)\) und \(C\,(-2|1|-3)\) folgt:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[a = \vert \overrightarrow C - \overrightarrow B \vert = \left| \begin {pmatrix} -2 - 6 \\ 1 - (-7) \\ -3 - 1 \end {pmatrix} \right| = \left| \begin {pmatrix} -8 \\ 8 \\ -4 \end {pmatrix} \right| = \sqrt{(-8)^2 + 8^2 + (-4)^2} = 12\]
\[b = \vert \overrightarrow C - \overrightarrow A \vert = \left| \begin {pmatrix} -2 - 1 \\ 1 - 7 \\ -3 - 3 \end {pmatrix} \right| = \left| \begin {pmatrix} -3 \\ -6 \\ -6 \end {pmatrix} \right| = \sqrt{(-3)^2 + (-6)^2 + (-6)^2} = 9\]
\[c = \vert \overrightarrow B - \overrightarrow A \vert = \left| \begin {pmatrix} 6 - 1 \\ -7 - 7 \\ 1 - 3 \end {pmatrix} \right| = \left| \begin {pmatrix} 5 \\ -14 \\ -2 \end {pmatrix} \right| = \sqrt{5^2 + (-14)^2 + (-2)^2} = 15\]
\[a^2 = c \cdot p \quad \Longleftrightarrow \quad p = \frac{a^2}{c}\]
\[b^2 = c \cdot q \quad \Longleftrightarrow \quad q = \frac{b^2}{c}\]
\[h^2 = p \cdot q \quad \Longleftrightarrow \quad h^2 = \frac{a^2 \cdot b^2}{c^2}\]
\[\Longrightarrow \quad r = h = \frac{a \cdot b}{c} = \frac{12 \cdot 9}{15} = 7{,}2\]
5. Lösungsansatz: Fläche des rechtwinkligen Dreiecks \(ABC\) bestimmen
Die Fläche des rechtwinkligen Dreiecks \(ABC\) lässt sich mit den Katheten \(\overline{AC}\) und \(\overline{BC}\) oder mit der Hypothenuse \(\overline{AB}\) und der Höhe \(h\) berechnen
Die Höhe \(h\) des rechtwinkligen Dreiecks \(ABC\) entspricht dem Radius \(r\) der beiden Kreise, die im Raum die Menge aller Punkte \(C^\ast\) der kongruenten Dreiecke \(ABC^\ast\) festlegen.
\(A = \frac{1}{2} \cdot \overline{AB} \cdot r \quad\) oder \(\quad A = \frac{1}{2} \cdot \overline{BC} \cdot \overline{AC}\)
\[\Longrightarrow \quad \overline{AB} \cdot r = \overline{BC} \cdot \overline{AC}\]
\[r = \frac{\overline{BC} \cdot \overline{AC}}{\overline{AB}} = \frac{a \cdot b}{c} = \frac{12 \cdot 9}{15} = 7{,}2\]