Im Koordinatensystem entspricht eine Längeneinheit 1 m, d.h. das Zimmer ist an seiner höchsten Stelle 3 m hoch.
Das Rechteck \(GHKL\) mit \(G\,(2|4|2)\) hat die Breite \(\overline{GL} = 1\,\). Es liegt in der Ebene \(E\), die Punkte \(H\) und \(K\) liegen auf der Geraden \(CD\,\). Das Rechteck stellt im Modell ein Dachfenster dar; die Breite des Fensterrahmens soll vernachlässigt werden.
Geben Sie die Koordinaten der Punkte \(L\), \(H\) und \(K\) an und bestimmen Sie den Flächeninhalt des Fensters.
(zur Kontrolle: \(\overline{GH} = \sqrt{5}\))
(5 BE)
Lösung zu Teilaufgabe c
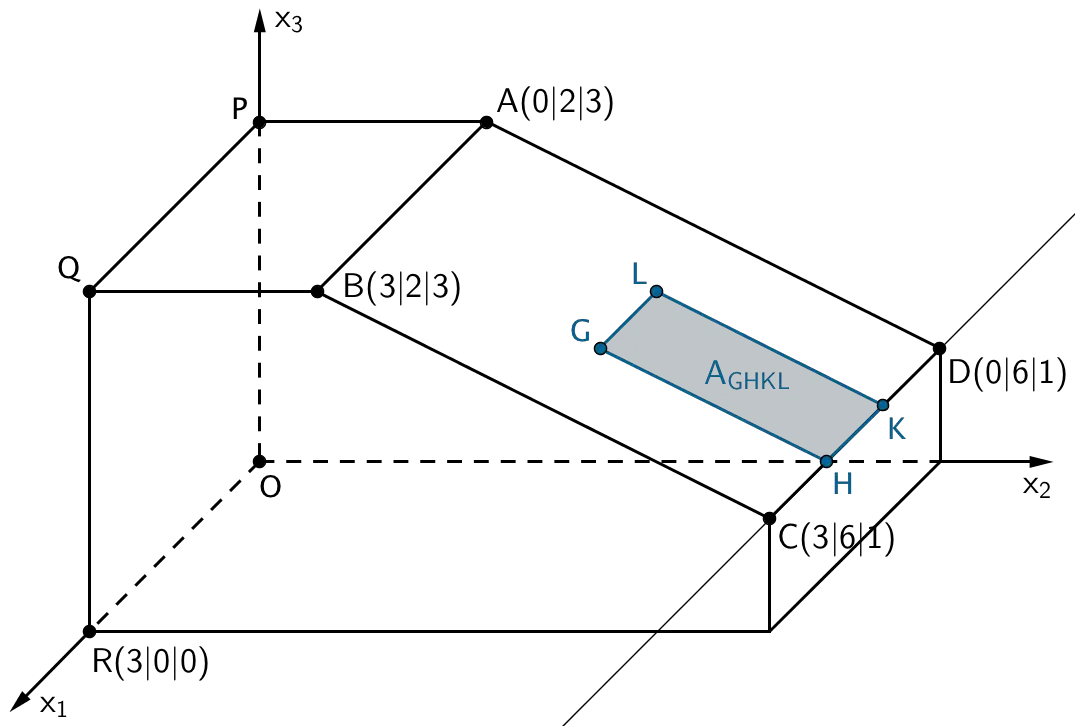
Rechteck \(\,GHKL\,\) (Dachfenster) und Gerade \(\,CD\,\)
\(G\,(2|4|2)\,\), \(\quad \overline{GL} = 1\,\), \(\quad H\,,K \in CD\)
Koordinaten der Punkte \(L\,,H\) und \(K\)
Da das Dachzimmer die Form eines geraden Prismas hat, der Boden und zwei Seitenwände in den Koordinatenebenen liegen, und das Fenster die Form eines Rechtecks hat, gilt:
\[GL \parallel x_1\text{-Achse}\,, \quad GH \perp CD\,, \quad LK \perp CD\]
Mithilfe von Abbildung 1 ergibt sich:
\[\overrightarrow{L} = \overrightarrow{G} + \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} + \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 4 \\ 2 \end{pmatrix} \quad \Longrightarrow \quad L\,(1|4|2)\]
\[\overrightarrow{H} = \overrightarrow{C} + \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 3 \\ 6 \\ 1 \end{pmatrix} + \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 6 \\ 1 \end{pmatrix} \quad \Longrightarrow \quad H\,(2|6|1)\]
\[\overrightarrow{K} = \overrightarrow{C} + \begin{pmatrix} -2 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 3 \\ 6 \\ 1 \end{pmatrix} + \begin{pmatrix} -2 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 6 \\ 1 \end{pmatrix} \quad \Longrightarrow \quad K\,(1|6|1)\]
Flächeninhalt des Fensters
\[\overrightarrow{GH} = \overrightarrow{H} - \overrightarrow{G} = \begin{pmatrix} 2 \\ 6 \\ 1 \end{pmatrix} - \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ -1 \end{pmatrix}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{GH} = \vert \overrightarrow{GH} \vert = \left| \begin{pmatrix} 0 \\ 2 \\ -1 \end{pmatrix} \right| = \sqrt{0^2 + 2^2 + (-1)^2} = \sqrt{5}\]
\[A_{GHKL} = \overline{GL} \cdot \overline{GH} = 1 \cdot \sqrt{5} = \sqrt{5} \approx 2{,}24\]
Der Flächeninhalt des Fensters beträgt ca. 2,24 m².


