Bestimmen Sie die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in \(H\) liegen.
(3 BE)
Lösung zu Teilaufgabe b
Mittelpunkt \(M\) der Strecke \([AC]\):
\[\overrightarrow{M} = \frac{1}{2} \cdot \left[ \begin{pmatrix}1\\2\\1 \end{pmatrix} + \begin{pmatrix}-3\\-6\\9 \end{pmatrix}\right] = \begin{pmatrix}-1\\-2\\5 \end{pmatrix}\]
Normalenvektor \(\overrightarrow{n}\) der Ebene \(H\):
\[H \colon 2x_1 + x_2 + 2x_3 - 6 = 0\; \Rightarrow \; \overrightarrow{n} = \begin{pmatrix} 2\\1\\2 \end{pmatrix}\]
\[\vert \overrightarrow{n} \vert = \sqrt{2^2+1^2+2^2} = 3\]
Und somit:
\[\overrightarrow{M} + 2 \cdot \overrightarrow{n} = \begin{pmatrix}-1\\-2\\5 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2\\1\\2 \end{pmatrix} = \begin{pmatrix} 3\\0\\9 \end{pmatrix}\]
Ausführliche Erklärung (nicht verlangt)
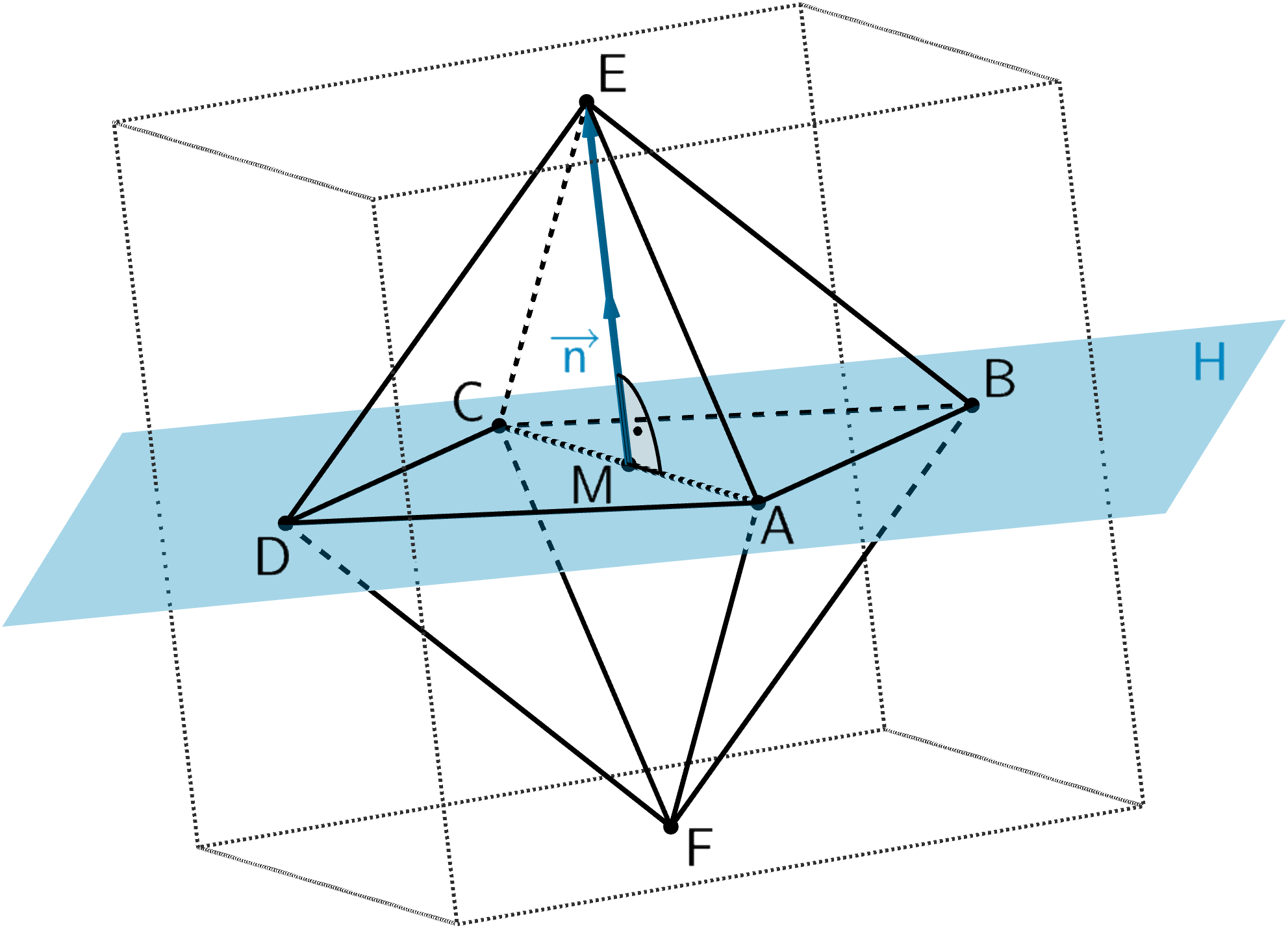
Die Punkte \(E\) und \(F\) liegen nicht in der Ebenen \(\textcolor{#0087c1}{H}\). Da der Würfel die Kantenlänge 12 hat (vgl. Teilaufgabe a), haben die Punkte \(E\) und \(F\) jeweils vom Mittelpunkt \(M\) der Strecke \([AC]\) den Abstand 6 LE (Längeneinheiten).
Beispielsweise ergibt sich der Ortsvektor \(\overrightarrow{E}\), indem man zum Ortsvektor \(\overrightarrow{M}\) ein geeignetes Vielfaches des Normalenvektors \(\textcolor{#0087c1}{\overrightarrow{n}}\) der Ebene \(H\) addiert.
\(\overrightarrow{E} = \overrightarrow{M} + k \cdot \textcolor{#0087c1}{\overrightarrow{n}}\) mit \(k \in \mathbb R^+\) und \(k \cdot \vert\textcolor{#0087c1}{\overrightarrow{n}}\vert = \textcolor{#cc071e}{6}\)
Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) der Strecke \([AC]\) berechnen:
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\overrightarrow{M} = \frac{1}{2} \cdot \Big(\overrightarrow{A} + \overrightarrow{C}\Big) = \frac{1}{2} \cdot \left[ \begin{pmatrix}1\\2\\1 \end{pmatrix} + \begin{pmatrix}-3\\-6\\9 \end{pmatrix}\right] = \begin{pmatrix}-1\\-2\\5 \end{pmatrix}\]
Normalenvektor \(\overrightarrow{n}\) der Ebene \(H\):
\[H \colon 2x_1 + x_2 + 2x_3 - 6 = 0\; \Rightarrow \; \textcolor{#0087c1}{\overrightarrow{n}} = \textcolor{#0087c1}{\begin{pmatrix} 2\\1\\2 \end{pmatrix}}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\vert \textcolor{#0087c1}{\overrightarrow{n}} \vert = \sqrt{2^2+1^2+2^2} = 3\]
Da der Normalenvektor \(\textcolor{#0087c1}{\overrightarrow{n}}\) die Länge \(3\) hat, wird zum Ortsvektor \(\overrightarrow{M}\) das Zweifache des Normalenvektors \(\textcolor{#0087c1}{\overrightarrow{n}}\) addiert, um den Ortsvektor \(\overrightarrow{E}\) zu berechnen.
\[\overrightarrow{E} = \overrightarrow{M} + 2 \cdot \textcolor{#0087c1}{\overrightarrow{n}} = \begin{pmatrix}-1\\-2\\5 \end{pmatrix} + 2 \cdot \textcolor{#0087c1}{\begin{pmatrix} 2\\1\\2 \end{pmatrix}} = \begin{pmatrix} 3\\0\\9 \end{pmatrix}\]


