Die Doppelpyramide wird so um die \(x\)-Achse gedreht, dass die Seitenfläche \(BCT\) in eine Fläche übergeht, die in der \(xy\)-Ebene liegt, und der Punkt \(S\) in einen Punkt \(S'\), der eine positive \(y\)-Koordinate hat. Abbildung 2 zeigt jeweils einen Längsschnitt der Doppelpyramide durch die \(yz\)-Ebene vor und nach dieser Drehung.
Begründen Sie anhand geeigneter Eintragungen in Abbildung 2, dass die \(y\)-Koordinate von \(S'\) den Wert \(24 \cdot \sin{\varphi}\) hat, wobei \(\varphi\) die in Aufgabe c bestimmte Winkelgröße ist.
 Abb. 2
Abb. 2
(2 BE)
Lösung zu Teilaufgabe f

Das Lot von \(S'\) auf die \(y\)-Achse bildet mit der Strecke \(\overline{TS'}\) ein rechtwinkliges Dreieck mit der Winkelgröße \(\textcolor{#cc071e}{\varphi}\) bei \(S'\).
Trigonometrische Beziehungen im rechtwinkligen Dreieck
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
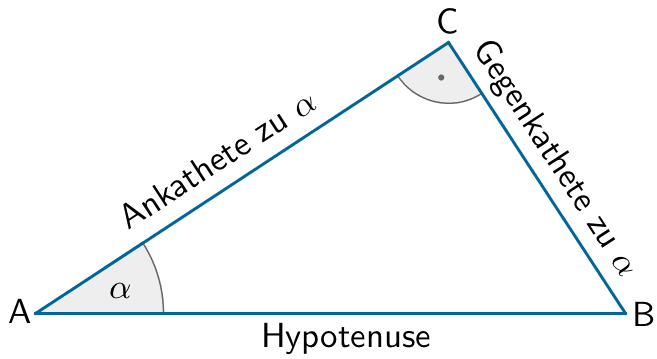
Es gilt: \(\sin{\textcolor{#cc071e}{\varphi}} = \dfrac{y_{S'}}{24} \; \Leftrightarrow \; y_{S'} = 24 \cdot \sin{\textcolor{#cc071e}{\varphi}}\)


