Das Saarpolygon wird mit verschiedenen Blickrichtungen betrachtet. Die Abbildungen 3 und 4 stellen das Saarpolygon für zwei Blickrichtungen schematisch dar.
 Abb. 3
Abb. 3
 Abb. 4
Abb. 4
Geben Sie zu jeder der beiden Abbildungen 3 und 4 einen möglichen Vektor an, der die zugehörige Blickrichtung beschreibet. Stellen Sie das Saarpolygon schematisch für eine Betrachtung von oben dar.
(4 BE)
Lösung zu Teilaufgabe f
Mögliche Vektoren
zu Abb. 3 sind z.B.: \(\begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix}\) oder \(\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\)
zu Abb. 4 sind z.B.: \(\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}\) oder \(\begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix}\)
Schematische Darstellung für eine Betrachtung von oben:


Ausführliche Beschreibung (nicht verlangt)
Möglicher Vektor, der die zugehörige Blickrichtung zu Abbildung 3 beschreibt
 Abb. 3
Abb. 3
Abbildung 3 zeigt, dass sich die Strecken \([AB]\) und \([CD]\) aus der zugehörigen Blickrichtung mittig kreuzen.
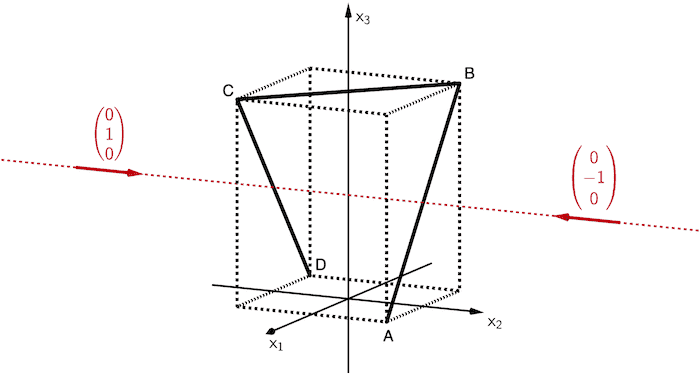
Die in Abbildung 3 gezeigte Ansicht entsteht, wenn der Blick frontal auf eine der Seitenflächen des Quaders gerichtet ist, welche die Diagonale \([AB]\) bzw. \([CD]\) enthält.
Ein Vektor, der die zugehörige Blickrichtung zu Abbildung 3 beschreibt, muss deshalb in Richtung der positiven oder negativen \(x_2\)-Achse zeigen.
Im einfachsten Fall kommen hierfür die Vektoren \(\textcolor{#cc071e}{\begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix}}\) oder \(\textcolor{#cc071e}{\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}}\) in Frage (schematische Darstellung).
Möglicher Vektor, der die zugehörige Blickrichtung zu Abbildung 4 beschreibt
 Abb. 4
Abb. 4
In Abbildung 4 ist die Strecke \([BC]\) aus der zugehörigen Blickrichtung nicht zu erkennen.
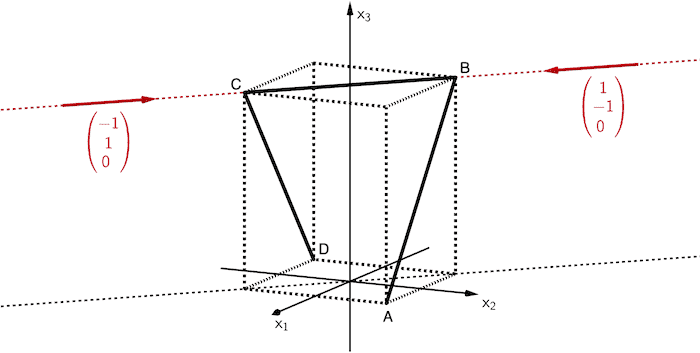
Die in Abbildung 4 gezeigte Ansicht entsteht, wenn der Blick in Richtung der Strecke \([BC]\) gerichtet ist.
Ein Vektor, der die zugehörige Blickrichtung zu Abbildung 4 beschreibt, muss analog zu den \(x_1\)- und \(x_2\)-Koordinaten von \(B(\textcolor{#cc071e}{-11}|\textcolor{#cc071e}{11}|28)\) und \(C(\textcolor{#cc071e}{11}|\textcolor{#cc071e}{-11}|28)\) in Richtung der Winkelhalbierenden zwischen der positiven \(x_1\)-Achse und der negativen \(x_2\)-Achse bzw. zwischen der negativen \(x_1\)-Achse und der positiven \(x_2\)-Achse zeigen (vgl. Abbildung 2).
Im einfachsten Fall kommen hierfür die Vektoren \(\textcolor{#cc071e}{\begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix}}\) oder \(\textcolor{#cc071e}{\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}}\) in Frage (schematische Darstellung).
Schematische Darstellung des Saarpolygons für eine Betrachtung von oben
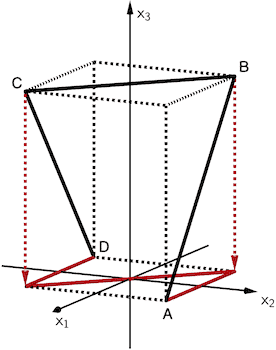
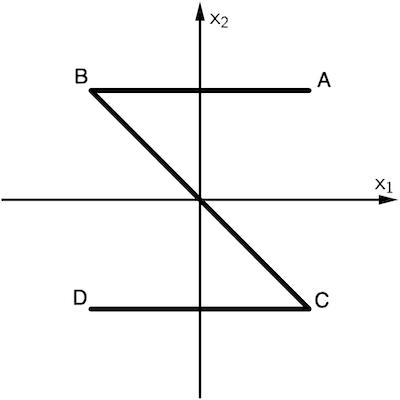
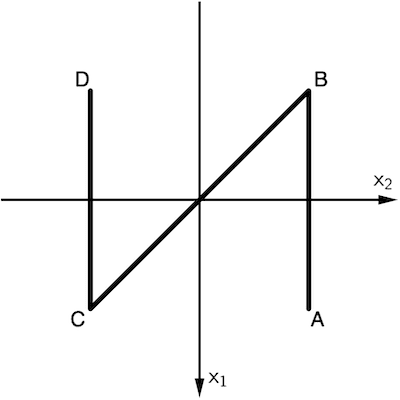
Ein Blick von oben projiziert die Punkte \(B\) und \(C\) in die \(x_1x_2\)-Ebene. Je nach Anordnung der \(x_1\)- und \(x_2\)-Achse ergibt die schematische Betrachtung von oben ein spiegelverkehrtes (liegendes) Z.


