Gegeben sind die Punkte \(A(-2|1|4)\) und \(B(-4|0|6)\)
Bestimmen Sie die Koordinaten des Punkts \(C\) so, dass gilt: \(\overrightarrow{CA} = 2 \cdot \overrightarrow{AB}\).
(2 BE)
Lösung zu Teilaufgabe 2a
Vektoraddition bzw. -subtraktion
1. Lösungsansatz: Vektorgleichung auflösen
\(A(-2|1|4)\), \(B(-4|0|6)\)
\[\overrightarrow{CA} = 2 \cdot \overrightarrow{AB}\]
\[\begin{align*}\overrightarrow{CA} &= 2 \cdot \overrightarrow{AB} \\[0.8em] \overrightarrow{A} - \overrightarrow{C} &= 2 \cdot \overrightarrow{AB} & &| + \overrightarrow{C} - 2 \cdot \overrightarrow{AB} \\[0.8em] \overrightarrow{A} - 2 \cdot \overrightarrow{AB} &= \overrightarrow{C} \\[0.8em] \overrightarrow{A} - 2 \cdot (\overrightarrow{B} - \overrightarrow{A}) &= \overrightarrow{C} \\[0.8em] \overrightarrow{A} - 2 \cdot \overrightarrow{B} + 2 \cdot \overrightarrow{A} &= \overrightarrow{C} \\[0.8em] 3 \cdot \overrightarrow{A} - 2 \cdot \overrightarrow{B} &= \overrightarrow{C} \\[0.8em] 3 \cdot \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} - 2 \cdot \begin{pmatrix} -4 \\ 0 \\ 6 \end{pmatrix} &= \overrightarrow{C} \\[0.8em] \begin{pmatrix} -6 \\ 3 \\ 12 \end{pmatrix} - \begin{pmatrix} -8 \\ 0 \\ 12 \end{pmatrix} &= \overrightarrow{C} \\[0.8em] \begin{pmatrix} 2 \\ 3 \\ 0 \end{pmatrix} &= \overrightarrow{C} \end{align*}\]
\[\Longrightarrow \quad C(2|3|0)\]
2. Lösungsansatz: Vektoraddition bzw. -subtraktion
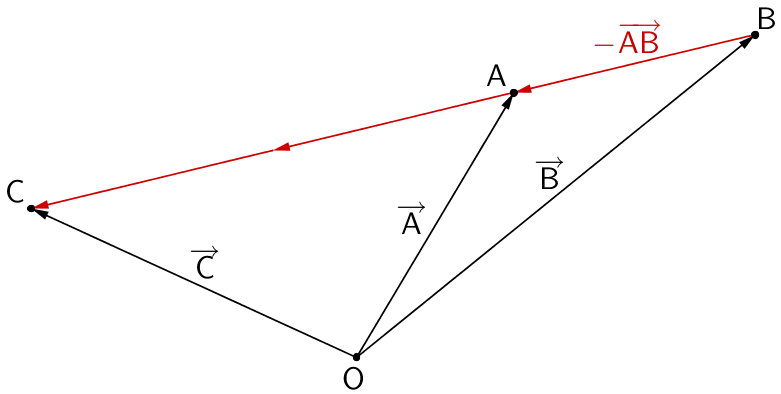
Planskizze: Ortsvektoren \(\overrightarrow{A}\), \(\overrightarrow{B}\) und \(\overrightarrow{C}\), Verbindungsvektor \(\overrightarrow{BA} = -\overrightarrow{AB}\) (Gegenvektor zu \(\overrightarrow{AB}\))
Die Koordinaten des Ortsvektors \(\overrightarrow{C}\) lassen sich durch Vektoraddition bzw. Subtraktion berechnen.
\(A(-2|1|4)\), \(B(-4|0|6)\)
\[\begin{align*} \overrightarrow{C} &= \overrightarrow{A} + 2 \cdot (-\overrightarrow{AB}) \\[0.8em] &= \overrightarrow{A} - 2 \cdot \overrightarrow{AB} \\[0.8em] &= \overrightarrow{A} - 2 \cdot (\overrightarrow{B} - \overrightarrow{A}) \\[0.8em] &= \overrightarrow{A} - 2 \cdot \overrightarrow{B} + 2 \cdot \overrightarrow{A} \\[0.8em] &= 3 \cdot \overrightarrow{A} - 2 \cdot \overrightarrow{B} \\[0.8em] &= 3 \cdot \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} - 2 \cdot \begin{pmatrix} -4 \\ 0 \\ 6 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -6 \\ 3 \\ 12 \end{pmatrix} - \begin{pmatrix} -8 \\ 0 \\ 12 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 \\ 3 \\ 0 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad C(2|3|0)\]
oder:

\(A(-2|1|4)\), \(B(-4|0|6)\)
\[\begin{align*} \overrightarrow{C} &= \overrightarrow{B} + 3 \cdot (-\overrightarrow{AB}) \\[0.8em] &= \overrightarrow{B} - 3 \cdot \overrightarrow{AB} \\[0.8em] &= \overrightarrow{B} - 3 \cdot (\overrightarrow{B} - \overrightarrow{A}) \\[0.8em] &= \overrightarrow{B} - 3 \cdot \overrightarrow{B} + 3 \cdot \overrightarrow{A} \\[0.8em] &= 3 \cdot \overrightarrow{A} - 2 \cdot \overrightarrow{B} \\[0.8em] &= 3 \cdot \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} - 2 \cdot \begin{pmatrix} -4 \\ 0 \\ 6 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -6 \\ 3 \\ 12 \end{pmatrix} - \begin{pmatrix} -8 \\ 0 \\ 12 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 \\ 3 \\ 0 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad C(2|3|0)\]


