Bestimmen Sie die Koordinaten von \(N\) und \(L\).

(Teilergebnis: \(N\,(7{,}2|8|7)\))

(4 BE)

Lösung zu Teilaufgabe f

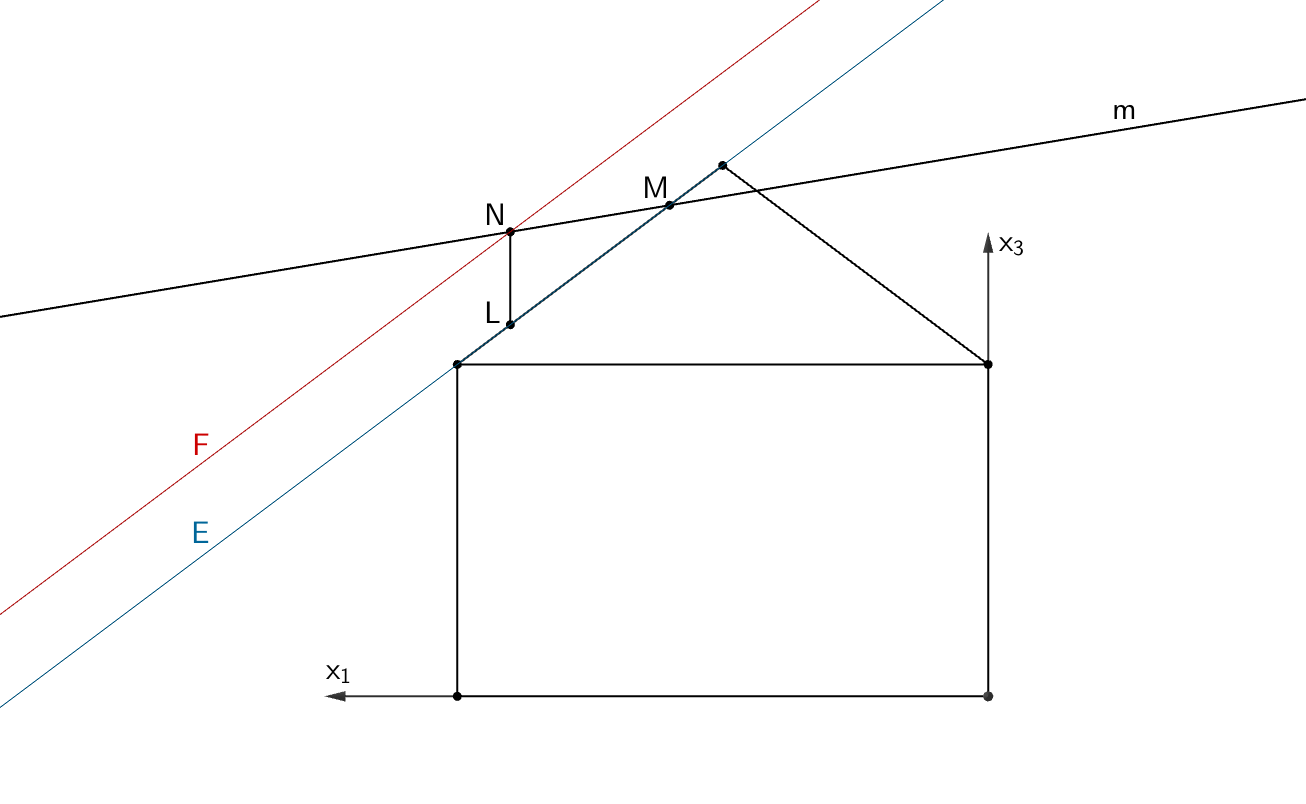
Die Gerade \(m\) schneidet die Ebene \(F\) im Punkt \(N\).

\(m\,\colon\,\overrightarrow{X} = \begin{pmatrix} 4{,}8 \\ 8 \\ 7{,}4 \end{pmatrix} + \mu \cdot \begin{pmatrix} 6 \\ 0 \\ -1 \end{pmatrix}\) (siehe Teilaufgabe e)

\(F\,\colon\,3x_{1} + 4x_{3} - 49{,}6 = 0\;\) (siehe Teilaufgabe e)

\[\begin{align*} m \cap F \,\colon\, 3 \cdot (4{,}8 + 6\mu) + 4 \cdot (7{,}4 - \mu) - 49{,}6 &= 0 \\[0.8em] 14{,}4 + 18\mu + 29{,}6 - 4\mu - 49{,}6 &= 0 \\[0.8em] -5{,}6 + 14\mu &= 0 & &| + 5{,}6 \\[0.8em] 14\mu &= 5{,}6 & &| : 14 \\[0.8em] \mu &= 0{,}4 \end{align*}\]

\[N \in m\,\colon\, \overrightarrow{N} = \begin{pmatrix} 4{,}8 \\ 8 \\ 7{,}4 \end{pmatrix} + 0{,}4 \cdot \begin{pmatrix} 6 \\ 0 \\ -1 \end{pmatrix} = \begin{pmatrix} 7{,}2 \\ 8 \\ 7 \end{pmatrix}\]

\[\Longrightarrow \quad N\,(7{,}2|8|7)\]

Der Punkt \(L\) liegt senkrecht um 1,4 tiefer unter dem Punkt \(N\) (siehe Angabe zu Teilaufgabe e).

\[\Longrightarrow \quad L\,(7{,}2|8|5{,}6)\]