Einer der folgenden Terme nähert den Term der in \(\mathbb R \, \backslash \{0\}\) definierten Funktion \(u \,\colon x \mapsto \dfrac{1}{x} + x + 1\) für große Werte von \(x\) am besten. Geben Sie diesen Term an und machen Sie Ihre Antwort plausibel.

\(\textsf{I} \enspace \dfrac{1}{x} \qquad \quad \)\(\textsf{II} \enspace x \qquad \quad \)\(\textsf{III} \enspace x + 1 \qquad \quad \)\(\textsf{IV} \enspace \dfrac{1}{x} + 1 \qquad \quad \)\(\textsf{V} \enspace \dfrac{1}{x} + x\)

(3 BE)

Lösung zu Teilaufgabe 4

Term III nähert die Funktion \(u(x) = \frac{1}{x} + x + 1\) für große Werte von \(x\) am besten.

1. Lösungsansatz: Verhalten von \(u\) für \(x\, \to\, \infty\)

\[\lim \limits_{x\, \to\, \infty} u(x) = \lim \limits_{x\, \to\, \infty} \underset{\to\,0}{\frac{1}{x}} + x + 1 = \lim \limits_{x\, \to\, \infty} x + 1  = \infty\]

Für \(x\, \to\, \infty\) unterscheiden sich die Funktionswerte von \(u(x)\) beliebig wenig von denen der Funktion \(v(x) = x + 1\), denn es gilt:

\[\lim \limits_{x\, \to\, \infty} \frac{1}{x} = 0\]

\(\Longrightarrow \quad y = x + 1\) ist schräge Asymptote von \(f(x)\).

\(\Longrightarrow \quad\) Term III nähert die Funktion \(u(x) = \frac{1}{x} + x + 1\) für große Werte von \(x\) am besten.

2. Lösungsansatz: Verhalten der Differenzfunktion \(d\) für \(x\,\to\,\infty\)

\[u(x) = \frac{1}{x} + x + 1\,; \quad v(x) = x + 1\]

\[d(x) = u(x) - v(x) = \frac{1}{x} + x + 1 - (x + 1) = \frac{1}{x}\]

Wenn sich die Funktion \(u\) für \(x\, \to\, \infty\) der Funktion \(v\) annähert, muss die Differenzfunktion \(d\) für \(x\,\to\,\infty\) gegen Null gehen.

\[\begin{align*} \lim \limits_{x\, \to\, \infty} d(x) = \lim \limits_{x\, \to\, \infty} \frac{1}{x} = 0 \end{align*}\]

\(\Longrightarrow \quad\) Term III nähert die Funktion \(u(x) = \frac{1}{x} + x + 1\) für große Werte von \(x\) am besten.

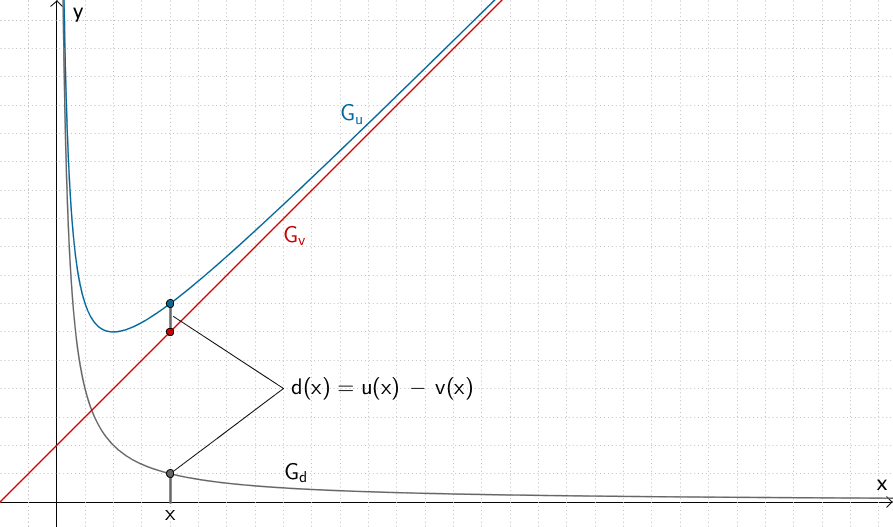
Für große Werte von \(x\) nähert sich der Graph von \(u\) der schrägen Asymptote \(v\, \colon \; y = x + 1\) an.