Eine vertikal stehende Getränkedose hat die Form eines geraden Zylinders. Die Lage des gemeinsamen Schwerpunkts \(S\) von Dose und enthaltener Flüssigkeit hängt von der Füllhöhe der Flüssigkeit über dem Dosenboden ab. Ist die Dose vollständig gefüllt, so beträgt die Füllhöhe 15 cm.

Die bisher betrachtete Funktion \(f\) gibt für \(0 \leq x \leq 15\) die Höhe von \(S\) über dem Dosenboden in Zentimetern an; dabei ist \(x\) die Füllhöhe in Zentimetern (vgl. Abbildung 3).

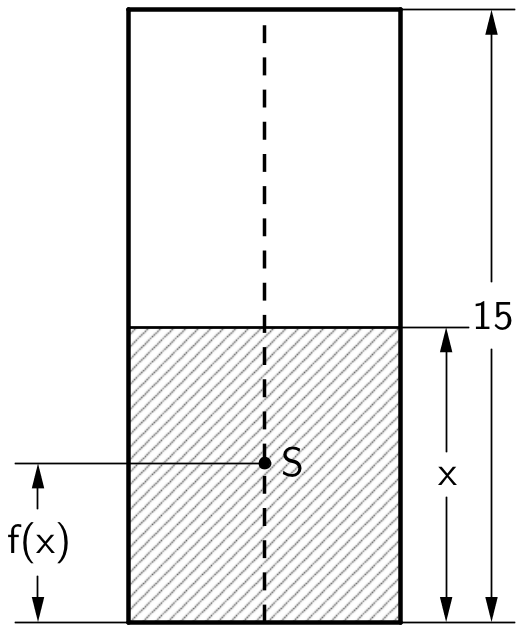
Abb. 3

Berechnen Sie \(f(0)\) und \(f(15)\). Interpretieren Sie die beiden Ergebnisse im Sachzusammenhang.

(3 BE)

Lösung zu Teilaufgabe 3a

\[f(x) = \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\,; \quad 0 \leq x \leq 15\]

Berechnung von \(f(0)\) und \(f(15)\)

\[f(0) = \frac{1}{2} \cdot 0 - \frac{1}{2} + \frac{8}{0 + 1} = -\frac{1}{2} + 8 = 7{,}5\]

\[f(15) = \frac{1}{2} \cdot 15 - \frac{1}{2} + \frac{8}{15 + 1} = 7{,}5 -\frac{1}{2} + \frac{1}{2} = 7{,}5\]

Interpretation der Ergebnisse im Sachzusammenhang

Sowohl bei einer leeren Dose \(f(0)\), als auch bei einer vollständig mit Flüssigkeit gefüllten Dose \(f(15)\), beträgt die Höhe des Schwerpunkts \(S\) über dem Dosenboden 7,5 cm. Der Schwerpunkt liegt dann mittig zur Höhe der Dose.

Der Verlauf von \(G_f\) für \(0 \leq x \leq 15\) zeigt, dass es sich bei den Funktionswerten \(f(0)\) und \(f(15)\) um Randmaxima handelt. Somit liegt der Schwerpunkt \(S\) für jede Füllhöhe \(0 < x < 15\) nieriger als 7,5 cm über dem Dosenboden.

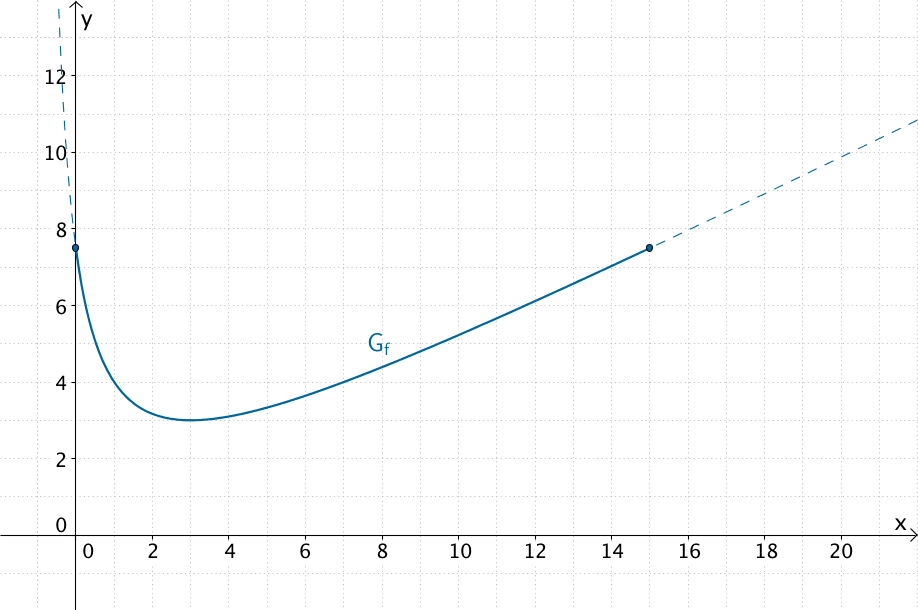
Verlauf des Graphen von \(f\) für \(0 \leq x \leq 15\) mit den Randmaxima \(f(0)\) und \(f(15)\)