Krümmungsverhalten
Das Krümmungsverhalten einer Funktion wird durch die zweite Ableitung beschrieben. Die erste Ableitung einer Funktion gibt die Steigung der Tangente an den Graphen der Funktion an (vgl. 1.5.1 Die Ableitung). Die zweite Ableitung, d.h. die Ableitung von der ersten Ableitung, gibt die Änderung (Zunahme oder Abnahme) der Steigung der Tangente an den Graphen der Funktion an, woraus sich auf das Krümmungsverhalten des Graphen schließen lässt.
Graphenkrümmung (vgl. Merkhilfe)
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad\) Der Graph \(G_{f}\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad\) Der Graph \(G_{f}\) ist in \(I\) linksgekrümmt.
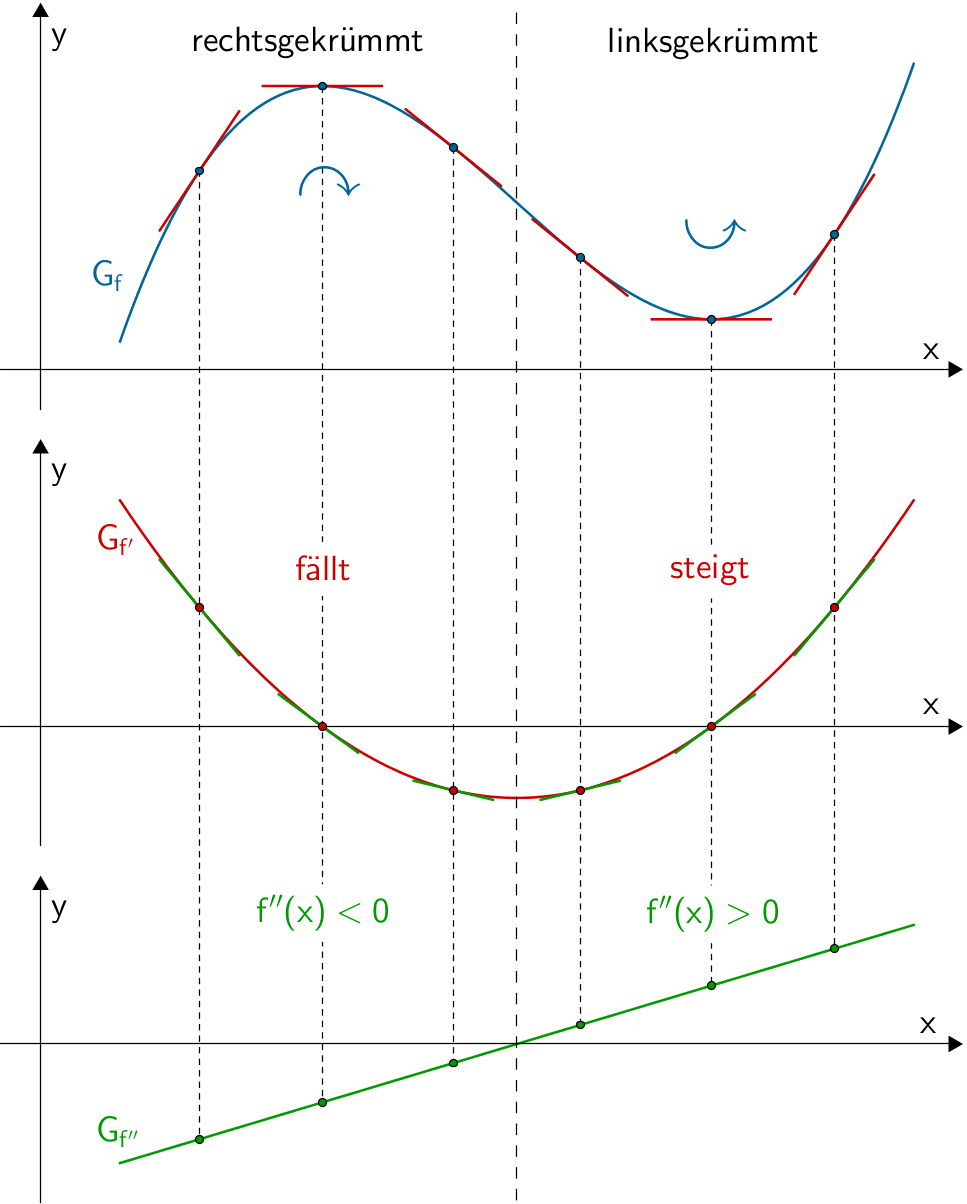
Ist der Graph rechtsgekrümmt (linksgekrümmt), nimmt die Steigung der Tangente an den Graphen der Funktion in Richtung der positiven \(x\)-Achse ab (zu). Die Tangente dreht sich rechtsherum (linksherum). Der Graph der ersten Ableitung fällt (steigt) und die Steigung der Tangente an den Graphen der ersten Ableitung ist negativ (positiv). Da die zweite Ableitung die Steigung der Tangente an den Graphen der ersten Ableitung beschreibt, gilt für eine Rechtskrümmung (Linkskrümmung): \(f''(x) < 0\) (\(f''(x) > 0\)).
Wendepunkte
An einer Wendestelle \(x_{0}\) wechselt der Graph einer Funktion das Krümmungsverhalten von rechtsgekrümmt nach linksgekrümmt oder umgekehrt. Der zugehörige Punkt \(W(x_{0}|f(x_{0}))\) heißt Wendepunkt. Die Tangente an den Graphen im Wendepunkt heißt Wendetangente \(w\). Die Wendetangente schneidet den Graphen im Wendepunkt.
Die Steigung der Tangente an den Graphen einer Funktion ist an einer Wendestelle \(x_{0}\) extremal (Wendetangente). Sie erreicht ein relatives Minimum (Wechsel von rechts- nach linksgekrümmt) oder ein relatives Maximum (Wechsel von links- nach rechtsgekrümmt). Der Graph der ersten Ableitung besitzt somit an der Wendestelle \(x_{0}\) eine Extremstelle mit waagrechter Tangente. Da die zweite Ableitung die Steigung der Tangente an den Graphen der ersten Ableitung angibt, gilt an einer Wendestelle: \(f''(x_{0}) = 0\).
An der Extremstelle der ersten Ableitung (Wendestelle) wechselt der Graph der ersten Ableitung das Monotonieverhalten (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte). Folglich muss an einer Wendestelle \(x_{0}\) die zweite Ableitung (Steigung der Tangente an den Graphen der ersten Ableitung) das Vorzeichen wechseln.
Wendepunkte (vgl. Merkhilfe)
Ist \(f''(x_{0}) = 0\) und wechselt \(f''\) an der Stelle \(x_{0}\) das Vorzeichen, so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) einen Wendepunkt.
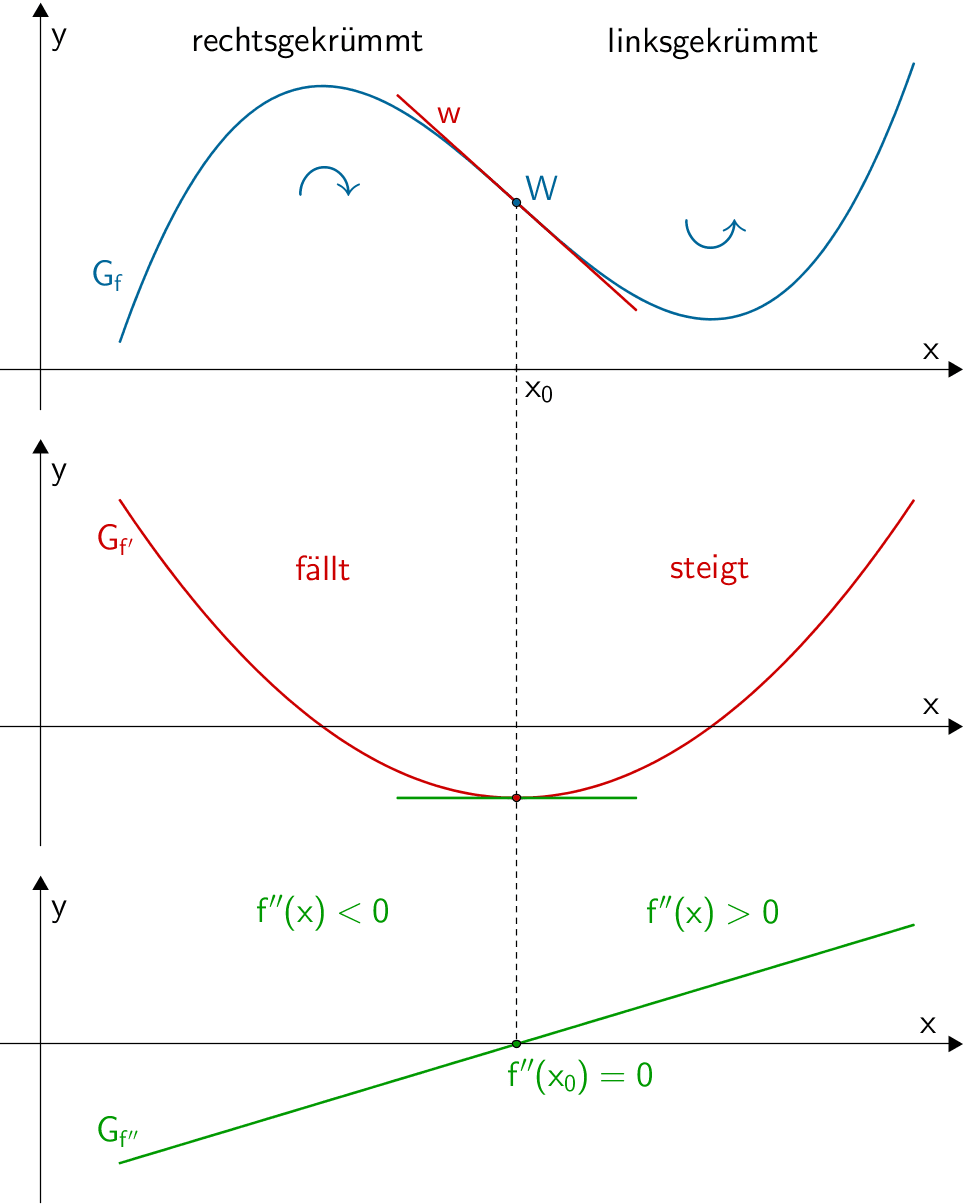
An der Wendestelle \(x_{0}\) ist die Steigung der Wendetangente \(w\) extremal und der Graph der Ableitung erreicht ein relatives Extremum mit waagrechter Tangente. Folglich gilt an der Wendestelle \(f''{x_{0}} = 0\) und ein Vorzeichenwechsel von \(f''\).
Veranschaulichung mithilfe einer Krümmungstabelle
| \(x < x_{0}\) | \(x = x_{0}\) | \(x > x_{0}\) | |
| \(f''(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\Large \curvearrowright\) | Wendepunkt | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) |
| \(x < x_{0}\) | \(x = x_{0}\) | \(x > x_{0}\) | |
| \(f''(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f}\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) | Wendepunkt | \(\Large \curvearrowright\) |
Bestimmung von Wendepunkten mithilfe der 3. Ableitung
Die Bedingungen \(f''(x_{0}) = 0\) und Vorzeichenwechsel von \(f''\) an der Stelle \(x_{0}\) bedeuten eine einfache Nullstelle der zweiten Ableitung. Die dritte Ableitung gibt die Steigung der Tangente an den Graphen der zweiten Ableitung an der Stelle \(x_{0}\) an. Diese muss zwangsläufig von Null verschieden sein.
Wendepunkte mithilfe der 3. Ableitung
Ist \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0 \), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) einen Wendepunkt.
Ergibt sich \(f'''(x_{0}) = 0\), ist keine Aussage möglich. Der Nachweis eines Wendepunkts mithilfe der dritten Ableitung hat den Nachteil, dass das Krümmungsverhalten in der Umgebung des Wendepunkts nicht erfasst wird.
Terrassenpunkte
Ein Terrassenpunkt \(TeP\) ist ein Wendepunkt mit einer waagrechten Wendetangente. Zusätzlich zu den Bedingungen für einen Wendepunkt \(W(x_{0}|f(x_{0}))\) gilt deshalb: \(f'(x_{0}) = 0\) (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
Terrassenpunkte
Ist \(f'(x_{0}) = f''(x_{0}) = 0\) und wechselt \(f''\) an der Stelle \(x_{0}\) das Vorzeichen, so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) einen Terrassenpunkt.
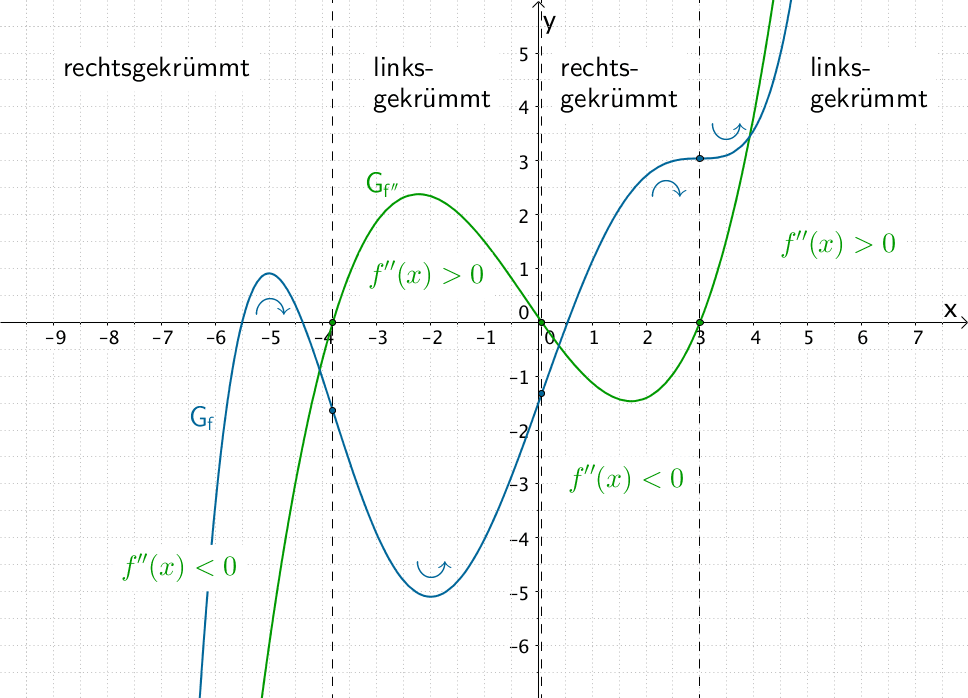
Wendepunkte, Terrassenpunkt und Krümmungsverhalten sowie Nullstellen und Vorzeichenwechsel der zweiten Ableitung am Beispiel des Graphen einer ganzrationalen Funktion \(f\)
Beispielaufgabe
Gegeben sei die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto \dfrac{3x}{x^{2} + 1}\). Bestimmen Sie die Lage der Wendepunkte des Graphen \(G_{f}\) der Funktion \(f\) und geben Sie das Krümmungsverhalten von \(G_{f}\) an.
\[f(x) = \frac{3x}{x^{2} + 1}; \; D_{f} = \mathbb R\]
Erste Ableitung \(f'\) und zweite Ableitung \(f''\) bilden:
Mithilfe der Quotientenregel, der Potenzregel, der Kettenregel, der Summenregel und der Faktorregel erhält man die erste Ableitung \(f'\) und die zweite Ableitung \(f''\) (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[\begin{align*} f'(x) &= \frac{3 \cdot (x^{2} + 1) - 3x \cdot 2x}{(x^{2} + 1)^{2}} \\[0.8em] &= \frac{3x^{2} + 3 - 6x^{2}}{(x^{2} + 1)^{2}} \\[0.8em] &= \frac{-3x^{2} + 3}{(x^{2} + 1)^{2}} \end{align*}\]
\[\begin{align*}f''(x) &= \frac{-6x \cdot (x^{2} + 1)^{2} - (-3x^{2} + 3) \cdot 2 \cdot (x^{2} + 1) \cdot 2x}{(x^{2} + 1)^{4}} \\[0.8em] &= \frac{\cancel{(x^{2} + 1)} \cdot \left[ -6x \cdot (x^{2} + 1) - (-3x^{2} + 3) \cdot 4x \right]}{\cancel{(x^{2} + 1)} \cdot (x^{2} + 1)^{3}} \\[0.8em] &= \frac{-6x^{3} - 6x + 12x^{3} - 12x}{(x^{2} + 1)^{3}} \\[0.8em] &= \frac{6x^{3} - 18x}{(x^{2} + 1)^{3}} \end{align*}\]
Notwendige Bedingung für Wendepunkte:
\[f''(x) \overset{!}{=} 0\]
\[\begin{align*} f''(x) = 0 \quad \Longrightarrow \quad 6x^{3} - 18x &= 0 \\[0.8em] 6x \cdot (x^{2} - 3) &= 0 \end{align*}\]
\[\begin{align*} \Longrightarrow \quad x_{1} = 0 \enspace \vee \enspace x^{2} - 3 &= 0 & &| + 3 \\[0.8em] x^{2} &= 3 & &| \; \sqrt{\enspace} \\[0.8em] x_{2,3} &= \pm \sqrt{3} \end{align*}\]
Nachweis des Vorzeichenwechsels der zweiten Ableitung sowie des Krümmungsverhaltens mithilfe einer Krümmungstabelle:
\[f''(x) = \frac{6x^{3} - 18x}{(x^{2} + 1)^{3}} = \frac{6x \cdot (x^{2} - 3)}{\underbrace{(x^{2} + 1)}_{> \, 0}}\]
Der Vorzeichenwechsel der zweiten Ableitung \(f''\) wird durch die Faktoren \(6x\) und \((x^{2} - 3)\) des Zählers bestimmt.
| \(x < -\sqrt{3}\) | \(x = -\sqrt{3}\) | \(-\sqrt{3} < x <0\) | |
| \(6x\) | \(-\) | \(-\) | \(-\) |
| \((x^{2} - 3)\) | \(+\) | \(0\) | \(-\) |
| \(f''(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\Large \curvearrowright\) | \(W\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) |
| \(-\sqrt{3} < x <0\) | \(0\) | \(0 < x < \sqrt{3}\) | |
| \(6x\) | \(-\) | \(0\) | \(+\) |
| \((x^{2} - 3)\) | \(-\) | \(-\) | \(-\) |
| \(f''(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f}\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) | \(W\) | \(\Large \curvearrowright\) |
| \(0 < x < \sqrt{3}\) | \(\sqrt{3}\) | \(\sqrt{3} < x\) | |
| \(6x\) | \(+\) | \(+\) | \(+\) |
| \((x^{2} - 3)\) | \(-\) | \(0\) | \(+\) |
| \(f''(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\Large \curvearrowright\) | \(W\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft}\) |
Lage der Wendepunkte:
\[f(x) = \frac{3x}{x^{2} + 1}; \; D_{f} = \mathbb R\]
\[f(-\sqrt{3}) = \frac{3 \cdot (-\sqrt{3})}{(-\sqrt{3})^{2} + 1} = -\frac{3}{4}\sqrt{3} \quad \Longrightarrow \quad W\bigg(-\sqrt{3}\,\bigg|-\frac{3}{4}\sqrt{3}\bigg)\]
\[f(0) = \frac{3 \cdot 0}{0^{2} + 1} = 0 \quad \Longrightarrow \quad W(0|0)\]
\[f(\sqrt{3}) = \frac{3 \cdot \sqrt{3}}{(\sqrt{3})^{2} + 1} = \frac{3}{4}\sqrt{3} \quad \Longrightarrow \quad W\bigg(\sqrt{3}\,\bigg|\frac{3}{4}\sqrt{3}\bigg)\]
Krümmungsverhalten des Graphen der Funktion \(f\):
Für \(x \in \; ]-\infty;-\sqrt{3}[\) ist \(G_{f}\) rechtsgekrümmt.
Für \(x \in \; ]-\sqrt{3}:0[\) ist \(G_{f}\) linksgekrümmt.
Für \(x \in \; ]0;\sqrt{3}[\) ist \(G_{f}\) rechtsgekrümmt.
Für \(x \in \; ]\sqrt{3};+\infty[\) ist \(G_{f}\) linksgekrümmt.
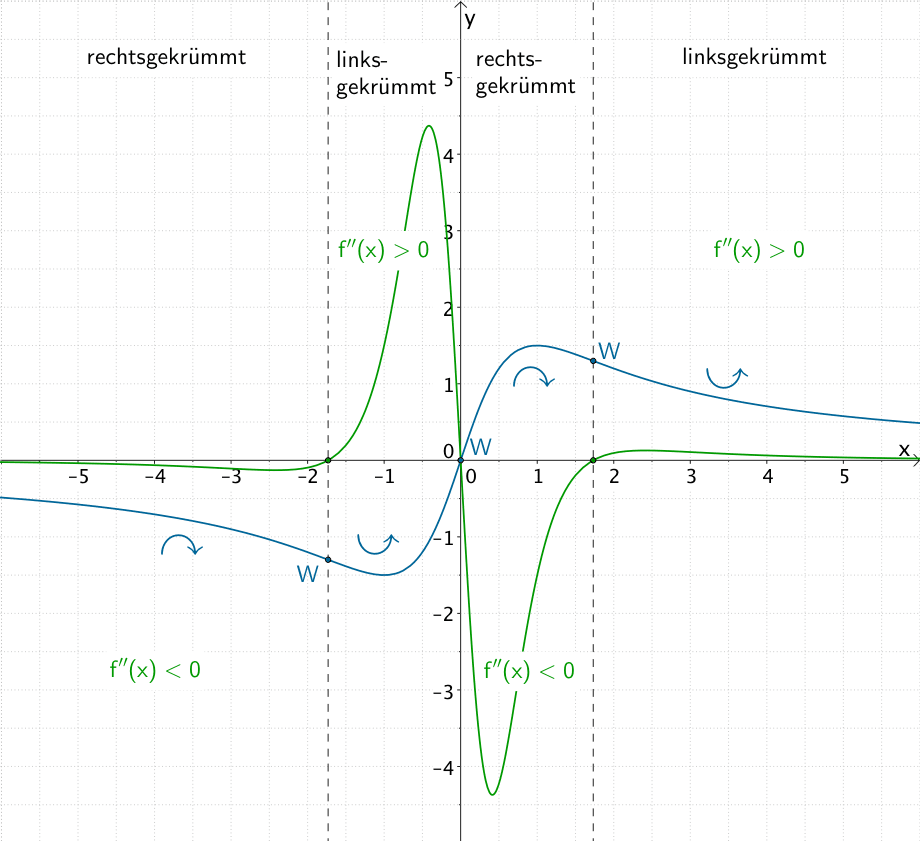
Graph der Funktion \(f \colon x \mapsto \dfrac{3x}{x^{2} + 1}\), Wendepunkte und Krümmungsverhalten


