Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind; machen Sie jeweils Ihre Entscheidung plausibel.
α) \(\lim \limits_{x\,\to\,-\infty} q(x) = +\infty\)
β) \(\lim \limits_{x\,\to\,+\infty} q(x) = 0\)
(4 BE)
Lösung zu Teilaufgabe 2e
\[q(x) = e^{-\frac{1}{4}x} \cdot \cos{x}\,; \quad D = \mathbb R\]
Aussage α)
Aussage α) ist falsch.
\[\lim \limits_{x\,\to\,-\infty}q(x) = \lim \limits_{x\,\to\,-\infty} \; \underbrace{e^{-\frac{1}{4}x}}_{\to\,+\infty} \cdot \underbrace{\cos{x}}_{[-1;1]}\]
Der Grenzwert \(\lim \limits_{x \, \to \, -\infty} q(x)\) existiert nicht.
Zwar gilt \(\lim \limits_{x \, \to \, -\infty} e^{-\frac{1}{4}x} = +\infty\), doch oszillieren die Werte der Kosinusfunktion zwischen \(-1\) und \(1\).
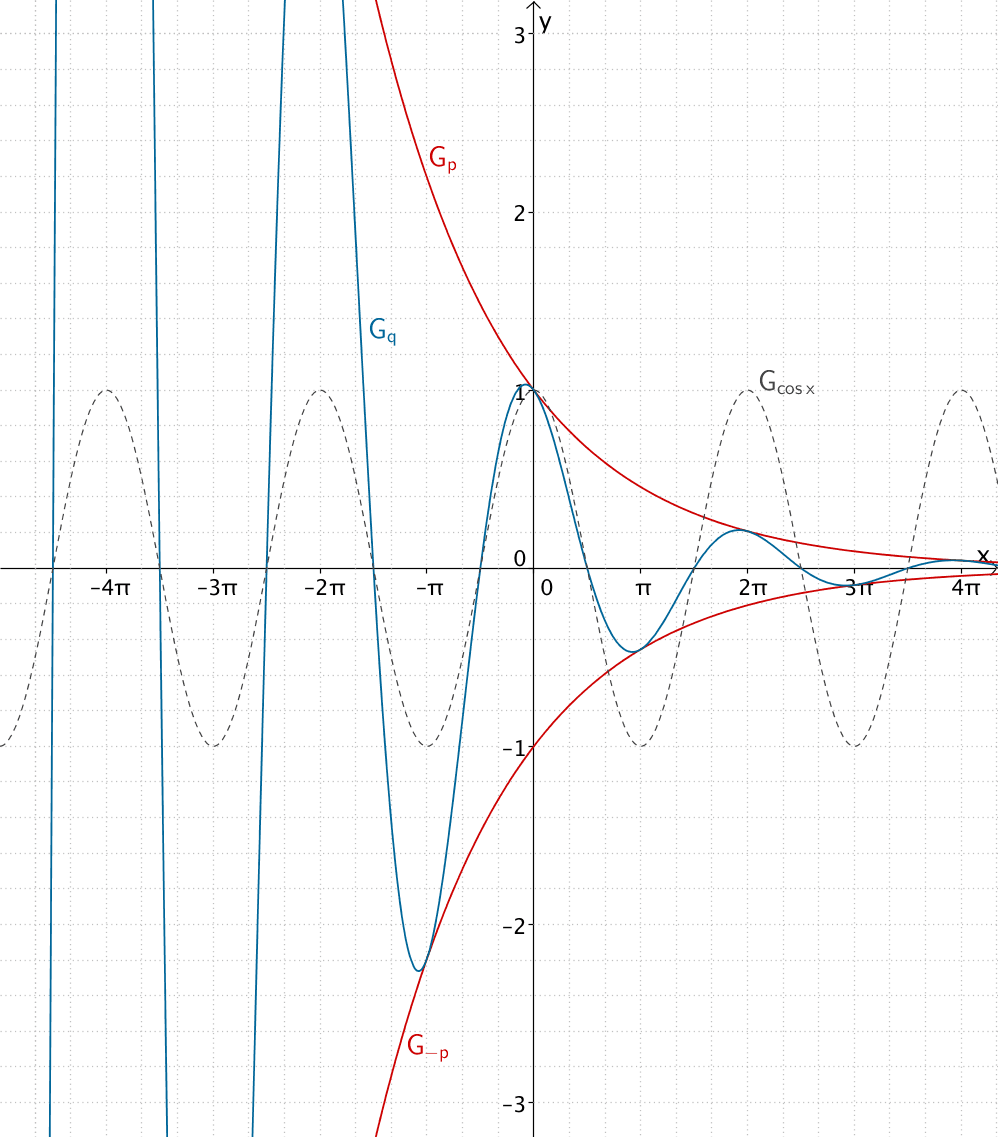
Für \(x \to -\infty\) existiert kein Grenzwert von \(q(x)\). Der Graph der Funktion \(q\) oszilliert zwischen den Graphen der Funktionen \(p\) und \(-p\).
Aussage β)
Aussage β) ist richtig.
\[\lim \limits_{x \, \to \, +\infty} q(x) = \lim \limits_{x \, \to \, +\infty} \, \underbrace{e^{-\frac{1}{4}x}}_{\to\,0} \cdot \cos x= 0\]
Der Graph der Funktion \(q\) nähert sich für \(x \, \to \, \infty\) der \(x\)-Achse an.
Für die Graphen der Funktionen \(p\) bzw. \(-p\), die \(G_q\) einschließen (siehe Teilaufgabe 2c), gilt:
\[\lim \limits_{x \, \to \, +\infty} p(x) = \lim \limits_{x \, \to \, +\infty} e^{-\frac{1}{4}x} = 0^+\]
\[\lim \limits_{x \, \to \, +\infty} -p(x) = \lim \limits_{x \, \to \, +\infty} -e^{-\frac{1}{4}x} = 0^-\]
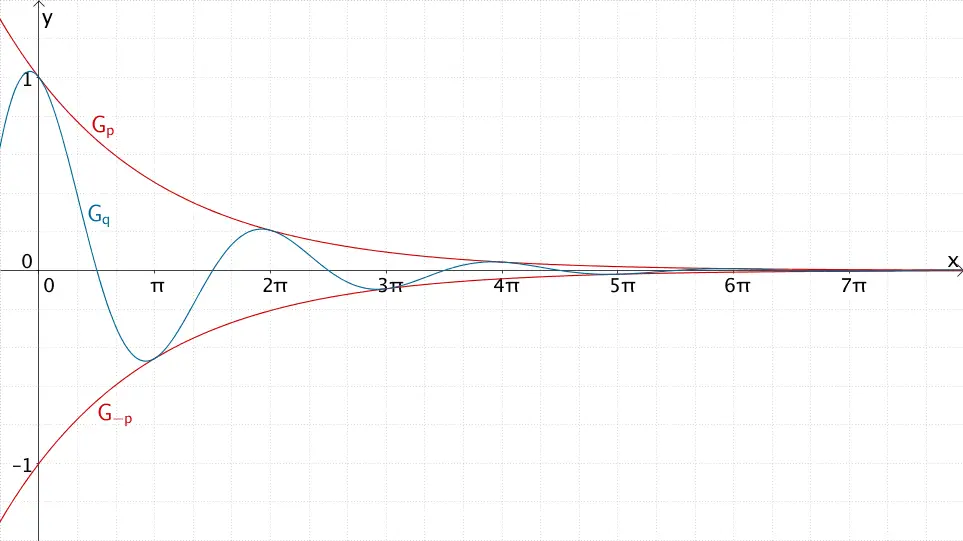
Für \(x \, \to \, +\infty\) nähert sich der Graph der Funktion \(q\) der \(x\)-Achse an.


