Geben Sie für \(a\), \(b\) und \(c\) alle Werte an, sodass sowohl \(D_{a,b,c} = \mathbb R\) gilt als auch, dass der Graph von \(f_{a,b,c}\) symmetrisch bezüglich des Koordinatenursprungs, aber nicht identisch mit der \(x\)-Achse ist.
(3 BE)
Lösung zu Teilaufgabe 2c
\[f_{\textcolor{#cc071e}{a},\textcolor{#0087c1}{b},\textcolor{#e9b509}{c}}(x) = \frac{\textcolor{#cc071e}{a}x + \textcolor{#0087c1}{b}}{x^{2} + \textcolor{#e9b509}{c}}\]
Damit \(D_{a,b,c} = \mathbb R\) ist, und der Graph von \(f_{a,b,c}\) symmetrisch bezüglich des Koordinatenursprungs, aber nicht identisch mit der \(x\)-Achse ist, muss
\(\textcolor{#cc071e}{a \neq 0}\) und
\(\textcolor{#0087c1}{b = 0}\) und
\(\textcolor{#e9b509}{c > 0}\)
gelten.
Begründung (nicht verlangt)
Die gebrochenrationalen Funktionen \(f_{a,b,c}\) sind in \(\mathbb R\) definiert, wenn der Nenner \(\boldsymbol{x^{2} + \textcolor{#e9b509}{c}}\) keine Nullstelle(n) und somit \(f_{a,b,c}\) keine Definitionslücke(n) hat. Folglich muss \(\textcolor{#e9b509}{c > 0}\) gelten.
\[x^{2} + \textcolor{#e9b509}{c} \neq 0 \enspace \Rightarrow \enspace \textcolor{#e9b509}{c > 0}\]
\[\Rightarrow \enspace f_{\textcolor{#cc071e}{a},\textcolor{#0087c1}{b},\textcolor{#e9b509}{c}}(x) = \frac{\textcolor{#cc071e}{a}x + \textcolor{#0087c1}{b}}{x^{2} + \textcolor{#e9b509}{c}}; \; \textcolor{#e9b509}{c > 0}\]
Die Graphen der Funktionen \(f_{a,b,c}\) mit \(\textcolor{#e9b509}{c > 0}\) sind bezüglich des Koordinatenursprungs punktsymmetrisch, wenn \(f_{a,b,c}(-x) = -f_{a,b,c}(x)\) gilt. Das bedeutet, dass der Zähler \(\boldsymbol{\textcolor{#cc071e}{a}x + \textcolor{#0087c1}{b}}\) für \(x < 0\) einen Vorzeichenwechsel haben muss (Nenner \(x^{2} + \textcolor{#e9b509}{c} > 0\)). Dies ist nur für \(\textcolor{#0087c1}{b = 0}\) der Fall.
Begründung durch Rechnung:
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
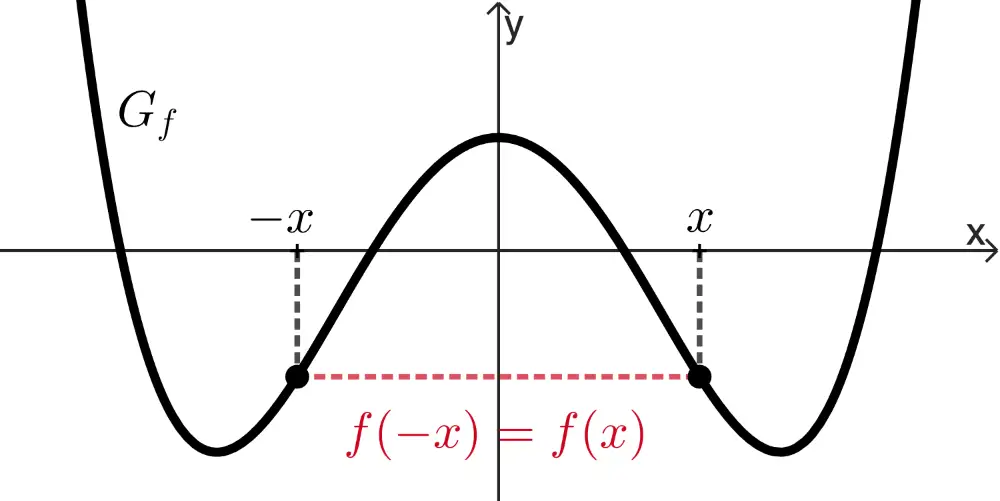
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
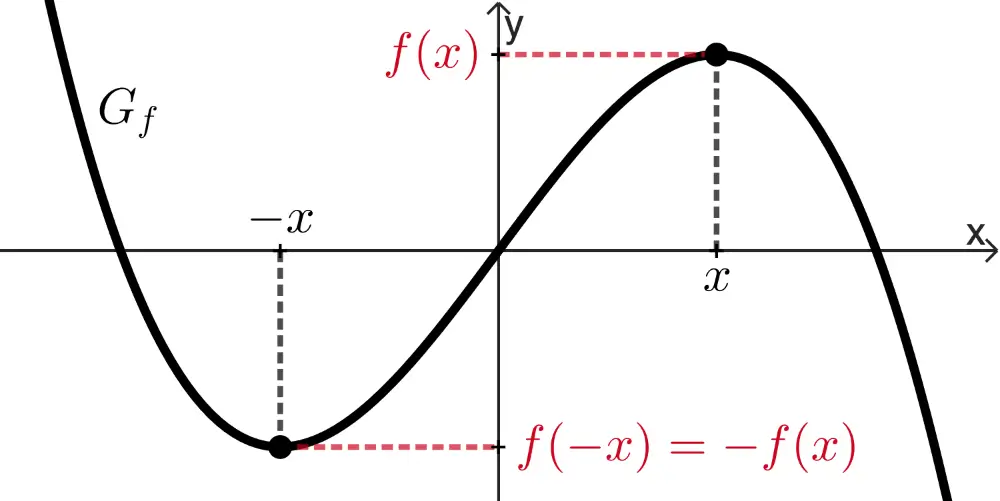
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[\begin{align*} f_{a,b,c}(-x) &= -f_{a,b,c}(x) \\[0.8em] \frac{a \cdot (-x) + b}{(-x)^{2} + c} &= -\frac{ax + b}{x^{2} + c} \\[0.8em] -\frac{ax - b}{x^{2} + c} &= -\frac{ax + b}{x^{2} + c} \\[0.8em] \Rightarrow \enspace \textcolor{#cc071e}{a}x - \textcolor{#0087c1}{b} &= \textcolor{#cc071e}{a}x + \textcolor{#0087c1}{b} &&| - \textcolor{#cc071e}{a}x \\[0.8em] -\textcolor{#0087c1}{b} &= +\textcolor{#0087c1}{b} \\[0.8em] \Rightarrow \enspace \textcolor{#0087c1}{b} &\textcolor{#0087c1}{=} \textcolor{#0087c1}{0}\end{align*}\]
\[\Rightarrow \enspace f_{\textcolor{#cc071e}{a},\textcolor{#0087c1}{0},\textcolor{#e9b509}{c}}(x) = \frac{\textcolor{#cc071e}{a}x}{x^{2} + \textcolor{#e9b509}{c}}; \; \textcolor{#e9b509}{c > 0}\]
Die Graphen der Funktionen \(f_{\textcolor{#cc071e}{a},\textcolor{#0087c1}{0},\textcolor{#e9b509}{c}}\) mit \(f_{\textcolor{#cc071e}{a},\textcolor{#0087c1}{0},\textcolor{#e9b509}{c}}(x) = \dfrac{\textcolor{#cc071e}{a}x}{x^{2} + \textcolor{#e9b509}{c}}; \; \textcolor{#e9b509}{c > 0}\) sind nicht identisch mit der \(\boldsymbol{x}\)-Achse \(\boldsymbol{(y = 0)}\), wenn der Zähler \(\boldsymbol{\textcolor{#cc071e}{a}x}\) ungleich null ist.
\[\textcolor{#cc071e}{a}x \neq 0 \enspace \Rightarrow \enspace \textcolor{#cc071e}{a \neq 0}\]
\[\Rightarrow \enspace f_{\textcolor{#cc071e}{a},\textcolor{#0087c1}{0},\textcolor{#e9b509}{c}}(x) = \frac{\textcolor{#cc071e}{a}x}{x^{2} + \textcolor{#e9b509}{c}}; \; \textcolor{#cc071e}{a \neq 0}, \; \textcolor{#e9b509}{c > 0}\]


