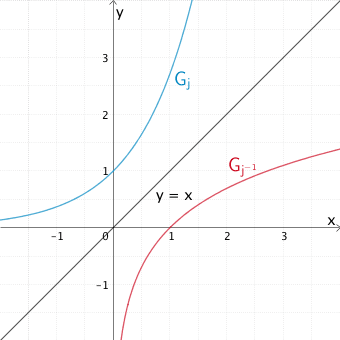Geben Sie den Term einer in \(\mathbb R\) definierten und umkehrbaren Funktion \(j\) an, die folgende Bedingungen erfüllt: Der Graph von \(j\) und der Graph der Umkehrfunktion von \(j\) haben keinen gemeinsamen Punkt.
(2 BE)
Lösung zu Teilaufgabe 4b
Zum Beispiel:
\(j(x) = x + 1\); \(j(x) = x - 1\); \(j(x) = x - 2\) usw.
oder
\(j(x) = e^{x}\) (mit Umkehrfunktion \(j^{-1}(x) = \ln{x}\))
Begründung (nicht verlangt)
Es kommt jede in \(\mathbb R\) definierte und umkehrbare Funktion \(j\) infrage, deren Graph keinen gemeinsamen Punkt mit der Winkelhalbierenden des I. und III. Quadranten hat. Denn dann existiert kein Fixpunkt der Spiegelung des Graphen von \(j\) an der Winkelhalbierenden, sodass der Graph von \(j\) und der Graph der Umkehrfunktion von \(j\) keinen gemeinsamen Punkt haben kann (vgl. Teilaufgabe 4a).
Dies trifft auf jede lineare Funktion \(j(x) = x + c\) mit \(c \in \mathbb R \backslash \{0\}\) zu, da deren Graphen (Geraden) parallel zur Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\) verlaufen.
Die Abbildung zeigt den Graphen \(\textcolor{#0087c1}{G_{j}}\) der Funktion \(\textcolor{#0087c1}{j(x) = x + 1}\) und den Graphen \(\textcolor{#cc071e}{G_{j^{-1}}}\) der Umkehrfunktion \(\textcolor{#cc071e}{j^{-1}(x) = x - 1}\), welche keinen gemeinsamen Punkt haben.
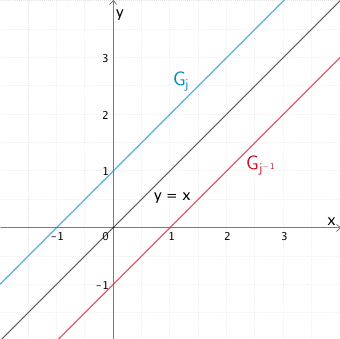
Aber auch der Graph \(\textcolor{#0087c1}{G_{j}}\) der in \(\mathbb R\) definierten Natürlichen Exponentialfunktion \(\textcolor{#0087c1}{j(x) = e^{x}}\) hat mit der Winkelhalbierenden des I. und III. Quadranten keinen gemeinsamen Punkt, weshalb dieser mit dem Graphen \(\textcolor{#cc071e}{G_{j^{-1}}}\) der Umkehrfunktion \(\textcolor{#cc071e}{j^{-1}(x) = \ln{x}}\) ebenfalls keinen gemeinsamen Punkt hat.