Im Sachzusammenhang ist neben der Funktion \(f\) die in \(\mathbb R\) definierte Funktion \(s\) mit \(s(x) = \left( \frac{x}{4} \right)^2 \cdot (4 - x)^3 = -\frac{1}{16}x^5 + \frac{3}{4}x^4 - 3x^3 + 4x^2\) von Bedeutung.
Begründen Sie, dass die folgende Aussage richtig ist:
Die Staulänge kann für jeden Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion \(s\) angegeben werden.
Bestätigen Sie rechnerisch, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat.
(4 BE)
Lösung zu Teilaufgabe 1e
\[s'(x) = -\frac{5}{16}x^4 + 3x^3 - 9x^2 + 8x = f(x)\]
\[s(0) = \left( \frac{0}{4} \right)^2 \cdot (4 - 0)^3 = 0\]
Somit ist die Aussage richtig.
\[s(4) = \left( \frac{4}{4} \right)^2 \cdot (4 - 4)^3 = 0\]
Ausführliche Erklärung (nicht verlangt)
Begründung, weshalb die Aussage richtig ist
Allgemein gilt: Beschreibt eine Funktion den Wert einer Größe in Abhängigkeit von der Zeit, so beschreibt die erste Ableitung der Funktion die momentane Änderungsrate der Größe pro Zeiteinheit zu einem betrachteten Zeitpunkt.
Differentialquotient oder lokale bzw. momentane Änderungsrate
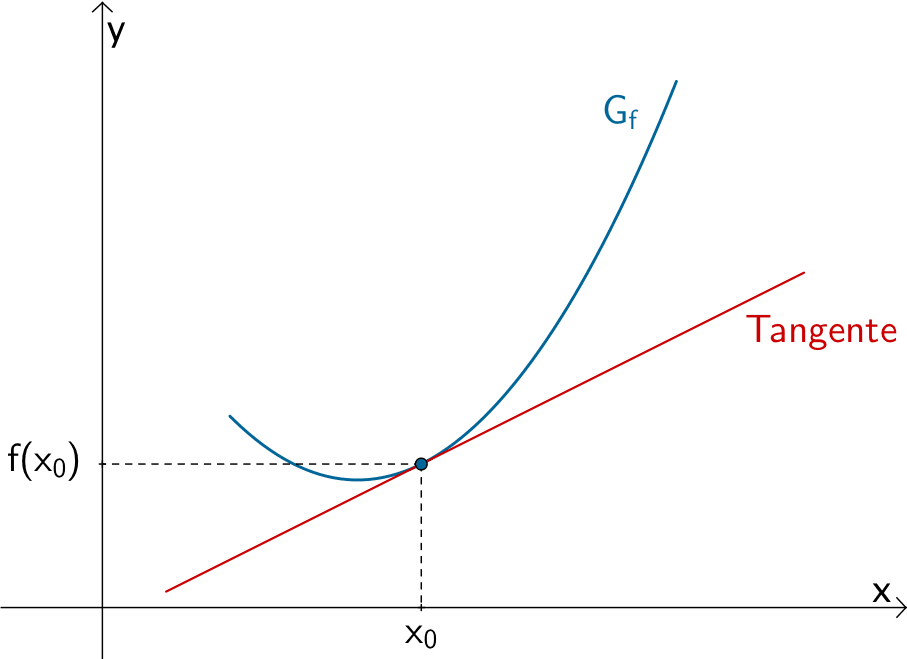
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Bei Aufgabe 1 beschreibt die Funktion \(f\) die momentane Änderungsrate der Staulänge in Kilometern pro Stunde (vgl. Angabe). Dann beschreibt eine bestimmte Stammfunktion von \(f\) die Staulänge in Kilometern in Abhängigkeit von der Zeit (\(f\) ist die erste Ableitung dieser Stammfunktion). Es ist zunächst also zu zeigen, dass \(s\) eine Stammfunktion von \(f\) ist, d. h. es ist \(s'(x) = f(x)\) nachzuweisen.
Stammfunktion
Eine differenzierbare Funktion \(F\) heißt eine Stammfunktion der Funktion \(f\), wenn für alle \(x \in D_f\) gilt:
\(F'(x) = f(x)\)
\[s(x) = -\frac{1}{16}x^5 + \frac{3}{4}x^4 - 3x^3 + 4x^2; \; D_s = \mathbb R\]
\[f(x) = -\frac{5}{16}x^4 + 3x^3 - 9x^2 + 8x; \; D_f = \mathbb R\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[\begin{align*}s'(x) &= -\frac{1}{16} \cdot 5 \cdot x^4 + \frac{3}{4} \cdot 4 \cdot x^3 - 3 \cdot 3 \cdot x^2 + 4 \cdot 2 \cdot x \\[0.8em] &= -\frac{5}{16}x^4 + 3x^3 - 9x^2 + 8x \\[0.8em] &= f(x)\end{align*}\]
Damit ist \(s\) eine Stammfunktion von \(f\).
Da der Stau erst um 06:00 Uhr entsteht und \(x\) die nach 06:00 Uhr vergangene Zeit in Stunden angibt (vgl. Angabe), ist \(s\) die im Sachzusammenhang korrekte Stammfunktion von \(f\), wenn zusätzlich \(s(0) = 0\) gilt.
\[s(\textcolor{#e9b509}{0}) = \left( \frac{\textcolor{#e9b509}{0}}{4} \right)^2 \cdot (4 - \textcolor{#e9b509}{0})^3 = 0 \cdot 4^3 = 0\]
Somit ist die Aussage
Die Staulänge kann für jeden Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion \(s\) angegeben werden.
richtig.
Rechnerische Bestätigung, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat
10:00 Uhr (4 Stunden nach 06:00 Uhr) entspricht \(x = 4\). Es ist \(s(4) = 0\) nachzuweisen.
\[s(\textcolor{#e9b509}{4}) = \left( \frac{\textcolor{#e9b509}{4}}{4} \right)^2 \cdot (4 - \textcolor{#e9b509}{4})^3 = 1 \cdot 0 = 0\]
Also hat sich der Stau um 10:00 Uhr vollständig aufgelöst.


