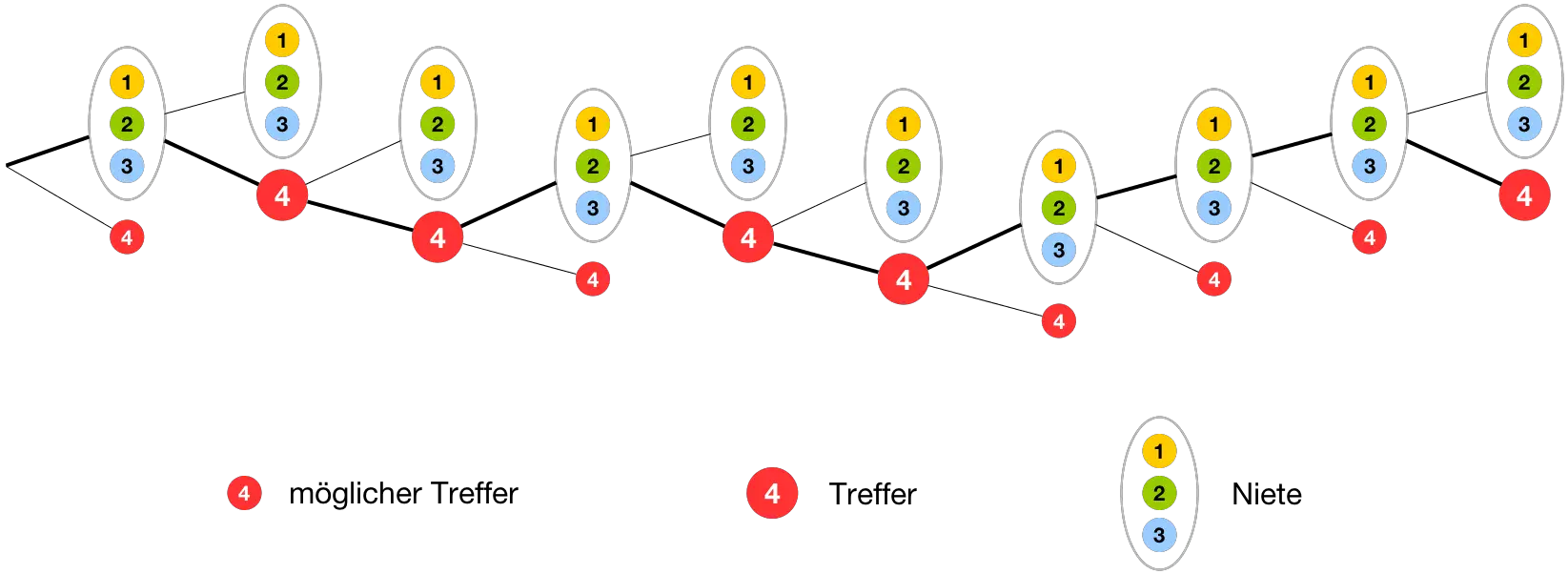
Zehn Besucher des Gemeindefests drehen nacheinander jeweils einmal das Glücksrad. Geben Sie zu jedem der folgenden Ereignisse einen Term an, mit dem sich die Wahrscheinlichkeit des Ereignisses berechnen lässt.
\(A\): "Nur die ersten fünf Preise entfallen auf die Kategorie 4."
\(B\): "Genau die Hälfte der Preise entfällt auf die Kategorie 4."
\(C\): "Die Preise verteilen sich jeweils zur Hälfte auf die Kategorien 1 und 4."
(5 BE)
Lösung zu Teilaufgabe 2b
Wahrscheinlichkeit \(P(A)\)
\(A\): "Nur die ersten fünf Preise entfallen auf die Kategorie 4."
Erläuterung mit Hilfe eines Baumdiagramms
Betrachtung der ersten fünf Drehungen des Glücksrads:
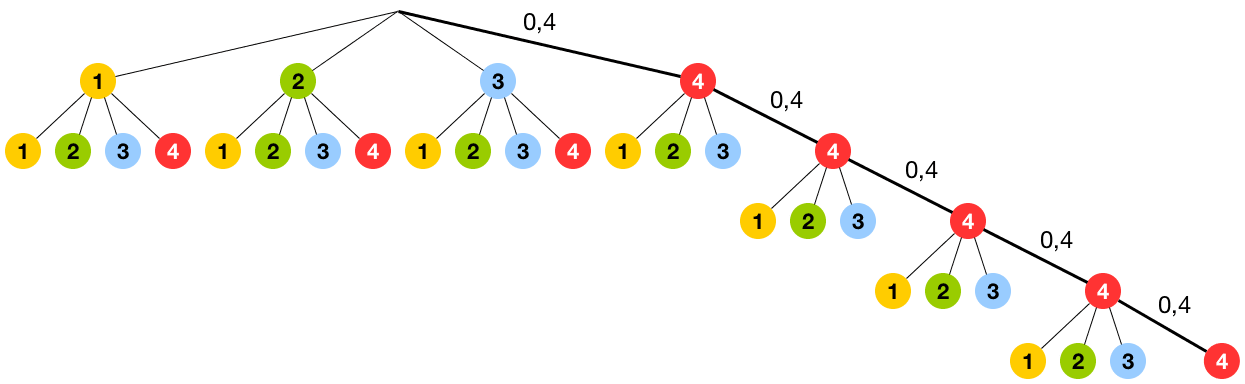
Die Abbildung zeigt den Pfad für das Ereignis "Die ersten fünf Preise entfallen auf Kategorie 4"
Die Wahrscheinlichkeit, dass ein Preis auf die Kategorie 4 entfällt, beträgt für jede Drehungen des Glücksrads \(P(\text{4}) = 0{,}4\) (siehe Teilaufgabe 2a).
Nach der 1. Pfadregel folgt:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P(5 \enspace \text{mal Kategorie 4}) = 0{,}4 \cdot 0{,}4 \cdot 0{,}4 \cdot 0{,}4 \cdot 0{,}4 = 0{,}4^5\]
Betrachtung der ersten fünf und der letzten fünf Drehungen des Glücksrads:
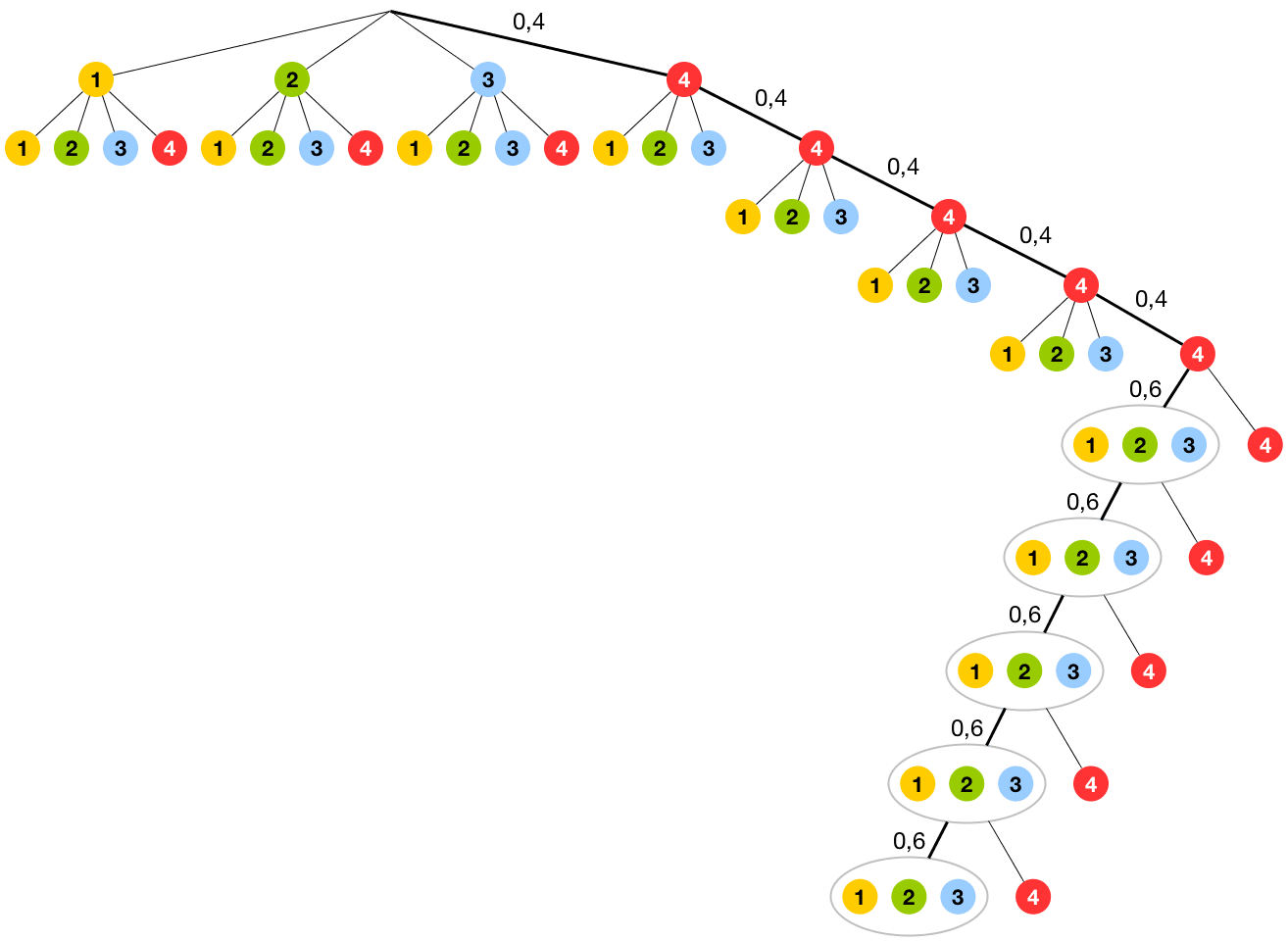
Die Abbildung zeigt den Pfad für das Ereignis \(A\): "Nur die ersten fünf Preise entfallen auf Kategorie 4"
Ab der 6. Drehung des Glücksrads sollen die Preise nicht mehr auf die Kategorie 4 entfallen, sondern auf die Kategorien 1, 2 oder 3. Die Wahrscheinlichkeit, dass ein Preis nicht auf die Kategorie 4 entfällt, beträgt dann bei den letzten \(5\) Drehungen jeweils:
\[P(\text{1, 2 oder 3}) = P(\overline{\text{4}}) = 1 - P(\text{4}) = 0{,}6\]
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Nach der 1. Pfadregel folgt:
\[P(5 \enspace \text{mal nicht Kategorie 4}) = 0{,}6 \cdot 0{,}6 \cdot 0{,}6 \cdot 0{,}6 \cdot 0{,}6 = 0{,}6^5\]
\[\Longrightarrow \quad P(A) = 0{,}4^5 \cdot 0{,}6^5\]
Wahrscheinlichkeit \(P(B)\)
\(B\): "Genau die Hälfte der Preise entfällt auf die Kategorie 4."
Es spielt keine Rolle, bei welcher Drehung des Glücksrads ein Preis auf die Kategorie 4 entfällt.
\(\Longrightarrow \quad\) Ohne Beachtung der Reihenfolge
Die Trefferwahrscheinlichkeit, dass ein Preis auf die Kategorie 4 entfällt, ist pro Drehung konstant (\(P(4) = 0{,}4\), siehe Teilaufgabe 2a).
\(\Longrightarrow \quad\) Mit Zurücklegen (bzw. Wiederholung)
Das Ereignis \(B\) unterscheidet nur zwei Ergebnisse: "Kategorie 4" (Treffer) und "nicht Kategorie 4" (Niete).
Jede der \(n = 10\) Drehungen des Glücksrads beschreibt dasselbe unabhängige Zufallsexperiment.
\(\Longrightarrow \quad\)Die Zufallsgröße \(X \;\colon \enspace\) "Anzahl der Preise, die auf die Kategorie 4 entfallen" ist nach \(B(10;\,0{,}4)\) binomialverteilt.
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
\[\begin {align*} P(B) &= P^{10}_{0{,}4}(X = 5) \\[0.8em] &= B(10;\,0{,}4;\,5) \\[0.8em] &= \binom{10}{5} \cdot 0{,}4^5 \cdot (1 - 0{,}4)^{10 - 5} \\[0.8em] &= \binom{10}{5} \cdot 0{,}4^5 \cdot 0{,}6^5 \end {align*}\]
Die Abbildung zeigt einen von \(\binom{10}{5} = 252\) möglichen Pfaden, die zusammen das Ereignis \(B\): "Genau die Hälfte der Preise entfällt auf die Kategorie 4" beschreiben.
Wahrscheinlichkeit \(P(C)\)
\(C\): "Die Preise verteilen sich jeweils zur Hälfte auf die Kategorien 1 und 4."
Es spielt keine Rolle, bei welcher Drehung des Glücksrads ein Preis auf die Kategorie 1 bzw. 4 entfällt.
\(\Longrightarrow \quad\) Ohne Beachtung der Reihenfolge
Im Gegensatz zum Ereignis \(B\), welches nur zwischen Treffer ("Kategorie 4") und Niete ("nicht Kategorie 4") unterscheidet, bedingnt das Ereignis \(C\) zwei konkrete Ergebnisse ("Kategorie 1", "Kategorie 4").
Erläuterung mit Hilfe eines Baumdiagramms
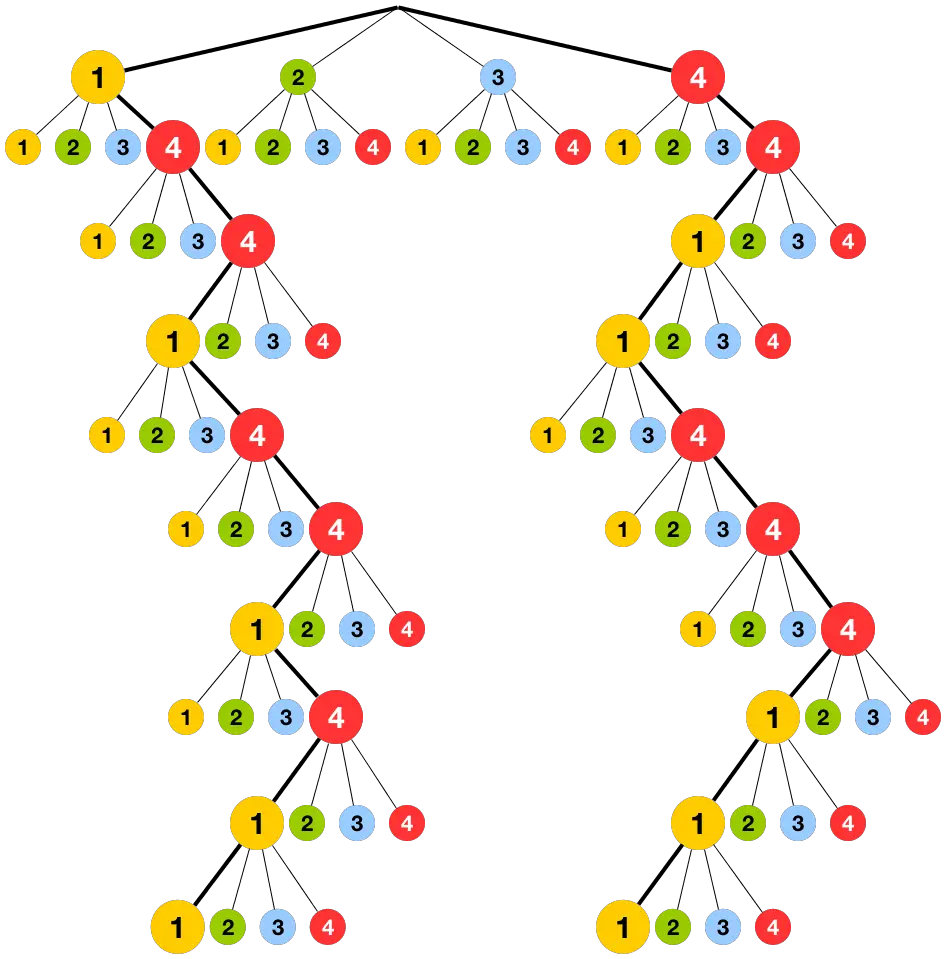
Die Abbildung zeigt zwei mögliche Pfade, die das Ereignis \(C\): "Die Preise verteilen sich jeweils zur Hälfte auf die Kategorien 1 und 4" beschreiben.
Jeder Pfad ist ein Ergebnis des Ereignisses \(C\). Nach der 1. Pfadregel folgt:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Linker Pfad: \( \hspace{9px} P = 0{,}1 \cdot 0{,}4 \cdot 0{,}4 \cdot 0{,}1 \cdot 0{,}4 \cdot 0{,}4 \cdot 0{,}1 \cdot 0{,}4 \cdot 0{,}1 \cdot 0{,}1 = 0{,}1^5 \cdot 0{,}4^5\)
Rechter Pfad: \(P = 0{,}4 \cdot 0{,}4 \cdot 0{,}1 \cdot 0{,}1 \cdot 0{,}4 \cdot 0{,}4 \cdot 0{,}4 \cdot 0{,}1 \cdot 0{,}1 \cdot 0{,}1 = 0{,}1^5 \cdot 0{,}4^5\)
Jeder der möglichen Pfade beschreibt die Wahrscheinlichkeit für eine bestimmte Abfolge der Kategorie 1 bzw. der Kategorie 4 bezogen auf die Reihenfolge der Drehungen des Glücksrads. Da das Ereignis \(C\) die Reihenfolge nicht berücksichtigt, müssen für die Bestimmung der Wahrscheinlichkeit \(P(C)\) alle möglichen Abfolgen der Kategorie 1 bzw. der Kategorie 4 berücksichtigt werden.
Mit Hilfe des Binomialkoeffizienten bestimmt man, wieviele Abfolgen (ohne Berücksichtigung der Reihenfolge) möglich sind.
Binomialkoeffizient
Der Binomialkoeffizient gibt an, wie viele Möglichkeiten es gibt, aus einer Menge mit \(n\) Elementen eine Teilmenge mit \(k\) Elementen zu bilden.
\[\binom{n}{k} = \frac{n!}{k! \cdot (n - k)!} = \frac{n \cdot (n - 1) \cdot ... \cdot (n - k + 1)}{k!}\]
(vgl. Merkhilfe)
Es gibt \(\binom{10}{5} = 252\) Möglichkeiten (Pfade), \(5\) mal die Kategorie 1 (oder \(5\) mal die Kategorie 4) auf \(10\) Drehungen des Glücksrads zu verteilen.
\[\Longrightarrow \quad P(C) = \binom{10}{5} \cdot 0{,}1^5 \cdot 0{,}4^5\]