Gegeben sind die in \(\mathbb R\) definierten Funktionen \(f\) und \(g\). Der Graph von \(f\) ist symmetrisch bezüglich der \(y\)-Achse, der Graph von \(g\) ist symmetrisch bezüglich des Koordinatenursprungs. Beide Graphen haben einen Hochpunkt im Punkt \((2|1)\).
- Geben Sie für die Graphen von \(f\) und \(g\) jeweils die Koordinaten und die Art eines weiteren Extrempunkts an.
(2 BE) - Untersuchen Sie die in \(\mathbb R\) definierte Funktion \(h\) mit \(h(x) = f(x) \cdot \left( g(x) \right)^3\) im Hinblick auf eine mögliche Symmetrie ihres Graphen.
(3 BE)
Lösung zu Aufgabe A5
a) Koordinaten und Art eines weiteren Extrempunkts der Graphen von \(f\) und \(g\)

Veranschaulichung durch eine Skizze: Beispiele für mögliche Graphen von \(f\) und \(g\) (nicht verlangt)
Ein weiterer Extrempunkt des Graphen von \(\textcolor{#0087c1}{f}\) ist der Hochpunkt \(\textcolor{#0087c1}{H(-2|1)}\).
Ein weiterer Extrempunkt des Graphen von \(\textcolor{#cc071e}{g}\) ist der Tiefpunkt \(\textcolor{#cc071e}{T(-2|-1)}\).
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
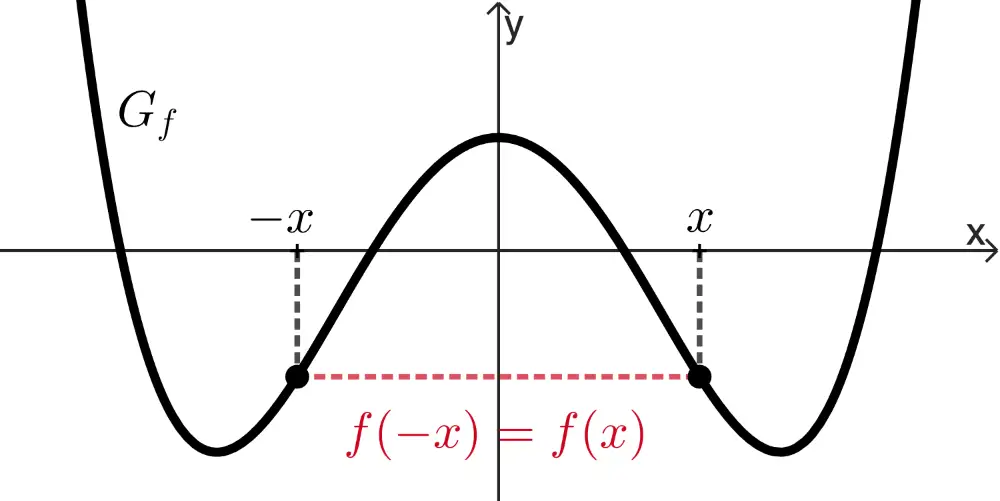
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
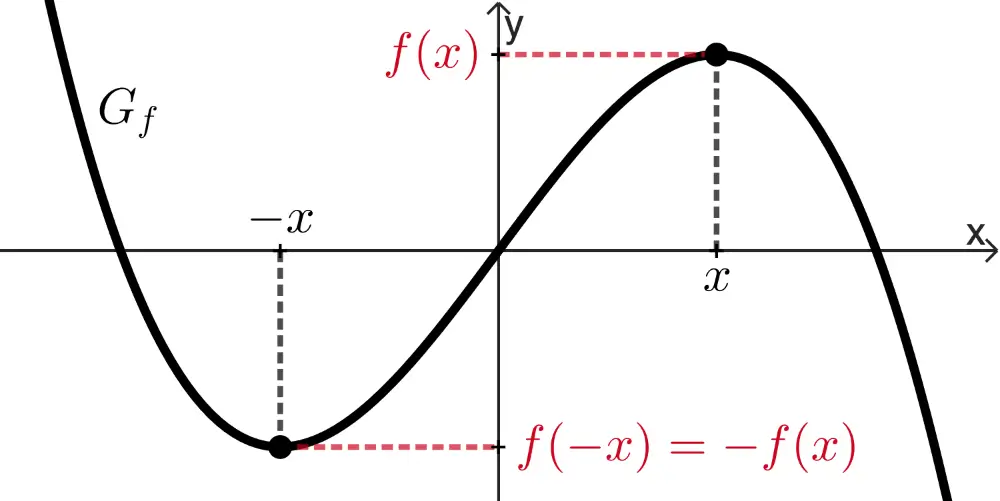
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
b) Untersuchung des Graphen von \(h\) auf eine mögliche Symmetrie
\[h(x) = f(x) \cdot \left(g(x)\right)^3; \; D_h = \mathbb R\]
Es wird \(h(-x)\) formuliert und überprüft, ob \(h(-x) = h(x)\) oder \(h(-x) = -h(x)\) oder keine der beiden Beziehungen zutrifft.
Dabei gilt \(f(-x) = f(x)\) wegen der Symmetrie von \(G_f\) bezüglich der \(y\)-Achse und \(g(-x) = -g(x)\) wegen der Symmetrie von \(G_g\) bezüglich des Koordinatenursprungs (vgl. Angabe).
\[\begin{align*}h(-x) &= f(-x) \cdot \left(g(-x)\right)^3 &&|\;f(-x) = f(x); \; g(-x) = -g(x) \\[0.8em] &= f(x) \cdot \left(-g(x)\right)^3 \\[0.8em] &= f(x) \cdot \left(-g(x)^3\right) \\[0.8em] &= -f(x) \cdot \left(g(x)\right)^3 \\[0.8em] &= -h(x)\end{align*}\]
Da \(h(-x) = -h(x)\) gilt, ist der Graph der Funktion \(h\) symmetrisch bezüglich des Koordinatenursprungs.
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.1.8 Symmetrie von Funktionsgraphen)


