Ermitteln Sie die \(x\)-Koordinate des Punkts, in dem der Graph von \(f\) eine waagrechte Tangente hat.
(4 BE)
Lösung zu Teilaufgabe 1b
Extremstelle einer Funktion bestimmen
\[f(x) = \frac{\ln{x}}{x^{2}}; \; D = \mathbb R^{+}\]
Die \(x\)-Koordinate des Punktes, in dem der Graph von \(f\) eine waagrechte Tangente hat (Steigung der Tangente ist gleich Null), ist die Extremstelle des Graphen von \(f\).
Notwendige Bedingung für eine Extremstelle des Graphen von \(f\):
\[f'(x) \overset{!}{=} 0\]
Erste Ableitung \(f'\) von \(f\) bilden:
Die Ableitung \(f'\) kann mithilfe der Quotientenregel, der Ableitung der natürlichen Logarithmusfunktion sowie der Ableitung einer Potenzfunktion bestimmt werden.
Quotientenregel
\[f(x) = \frac{u(x)}{v(x)} \quad \Longrightarrow \quad f'(x) = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]
Ableitung der natürlichen Logarithmusfunktion
\[f(x) = \ln x \enspace (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[f(x) = \frac{\ln{x}}{x^{2}}\]
\[\begin{align*}f'(x) &= \frac{\frac{1}{x} \cdot x^{2} - \ln{x} \cdot 2x}{\left( x^{2} \right)^{2}} \\[0.8em] &= \frac{x - \ln{x} \cdot 2x}{x^{4}} \\[0.8em] &= \frac{\cancel{x} \cdot (1 - 2 \ln{x})}{\cancel{x} \cdot x^{3}} \\[0.8em] &= \frac{1 - 2 \ln{x}}{x^{3}} \end{align*}\]
Nullstelle von \(f'\) bestimmen:
\[f'(x) = \frac{1 - 2 \ln{x}}{x^{3}} = 0\]
Zur Bestimmung der Nullstelle von \(f'\) wird die Nullstelle des Zählerterms \(1 - 2 \ln{x}\) ermittelt (Quotient ist gleich Null, wenn der Zähler gleich Null ist).
\[\begin{align*}1 - 2 \ln{x} &= 0 & &| + 2 \ln{x} \\[0.8em] 1 &= 2 \ln{x} & &| : 2 \\[0.8em] \frac{1}{2} &= \ln{x} & &| \; e^{(\dots)} \enspace \text{(zur Basis}\; e \; \text{potenzieren)} \\[0.8em] e^{\frac{1}{2}} &= e^{\ln{x}} & &| \; a^{\log_{a}{x}} = x \\[0.8em] e^{\frac{1}{2}} &= x & &| \; a^{\frac{1}{n}} = \sqrt[n]{a} \\[0.8em] \sqrt{e} &= x \end{align*}\]
Die \(x\)-Koordinate des Punktes, in dem der Graph von \(f\) eine waagrechte Tangente hat ist \(x = \sqrt{e}\).
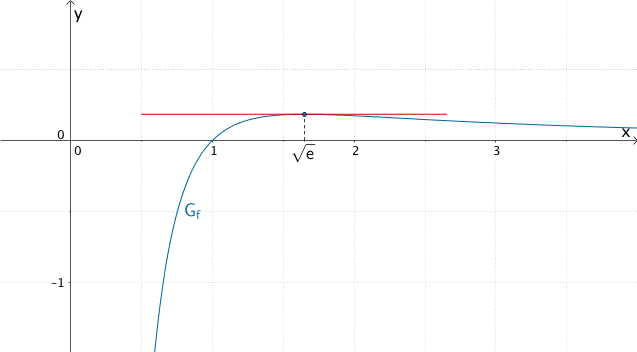
Extremstelle \(x = \sqrt{e}\) des Graphen der Funktion \(f\) (\(x\)-Koordinate des Punktes, in dem \(G_{f}\) eine waagrechte Tangente hat.)


