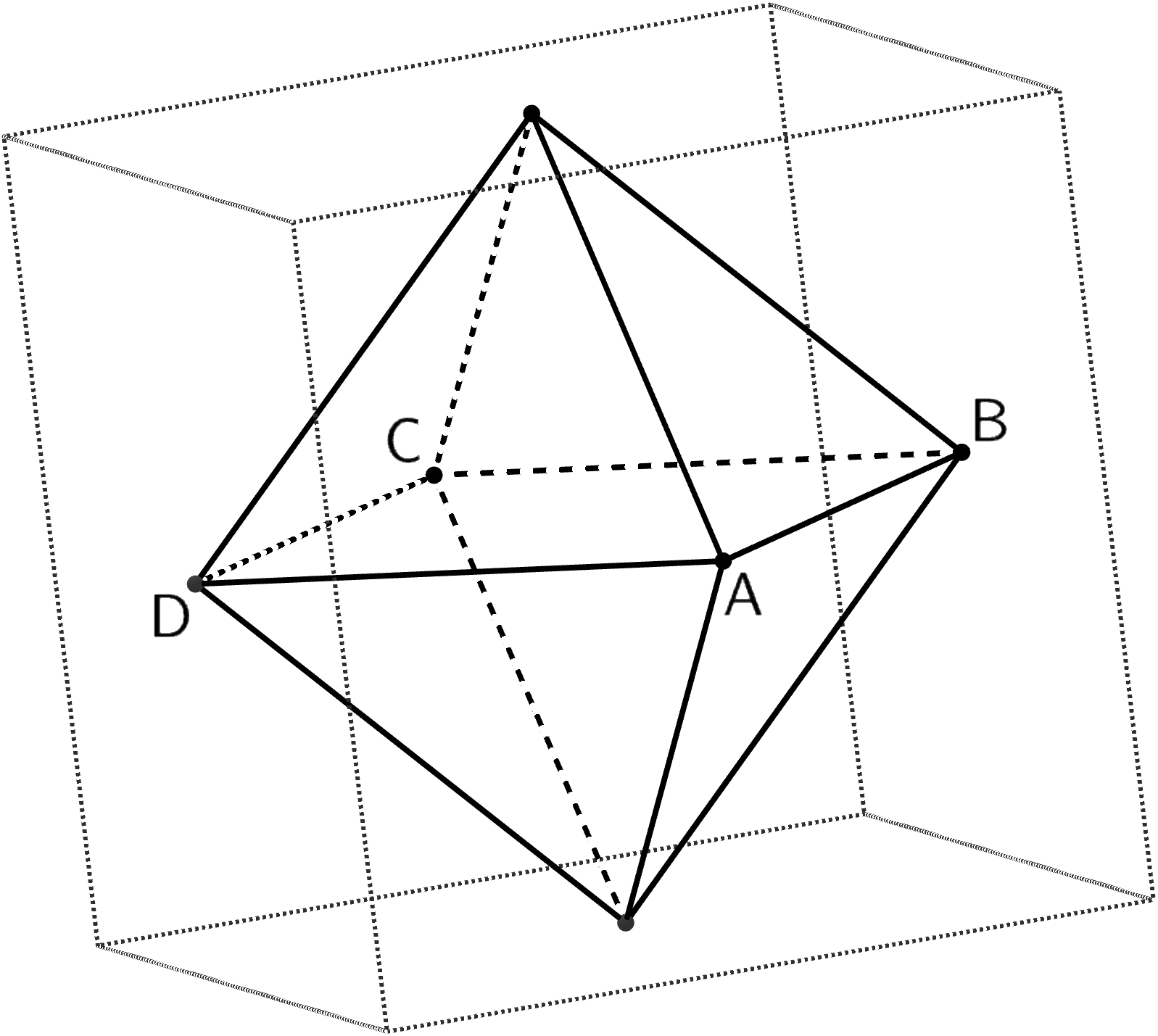
Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung). Die Eckpunkte \(A(1|2|1)\), \(B\), \(C(-3|-6|9)\) und \(D\) des Oktaeders liegen in der Ebene \(H\) mit der Gleichung \(2x_1 + x_2 + 2x_3 - 6 = 0\).
Weisen Sie nach, dass die Kantenlänge des Würfels 12 beträgt.
(2 BE)
Lösung zu Teilaufgabe a
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
Da die Punkt \(A\) und \(C\) die Mittelpunkte zweier gegenüberliegender Seitenflächen des Würfels sind, beschreibt die Strecke \([AC]\) den Abstand dieser Seitenflächen. Somit entspricht die Kantenlänge des Würfels der Länge der Strecke \(\textcolor{#cc071e}{[AC]}\).
\(A(1|2|1)\), \(C(-3|-6|9)\)
\[\begin{align*}\textcolor{#cc071e}{\overline{AC}} &= \vert \overrightarrow{AC} \vert = \vert \overrightarrow{C} - \overrightarrow{A} \vert = \left| \begin{pmatrix} -3 \\ -6 \\ 9 \end{pmatrix} - \begin{pmatrix} 1\\2\\1 \end{pmatrix} \right| = \left| \begin{pmatrix} -4\\-8\\8 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-4)^2 + (-8)^2 + 8^2} = \sqrt{16 + 64 + 64} = \sqrt{144} \\[0.8em] &= \textcolor{#cc071e}{12}\end{align*}\]
![Strecke [AC] und dazu parallele Kanten des Würfels](/images/stories/B2024_PT_A_G1_G2/B2024_PT_A_G1G2_a_web.png)


