In der Lungenfunktionsdiagnostig spielt der Begriff der Atemstromstärke eine wichtige Rolle.
Im Folgenden wird die Atemstromstärke als die momentane Änderungsrate des Luftvolumens in der Lunge betrachtet, d.h. insbesondere, dass der Wert der Atemstromstärke beim Einatmen positiv ist. Für eine ruhende Testperson mit normalem Atemrhythmus wird die Atemstromstärke in Abhängigkeit von der Zeit modellhaft durch die Funktion \(\displaystyle g \colon x \mapsto -\frac{\pi}{8} \sin \left( \frac{\pi}{2}t \right)\) mit Definitionsmenge \(\mathbb R_{0}^{+}\) beschrieben. Dabei ist \(t\) die seit Beobachtungsbeginn vergangene Zeit in Sekunden und \(g(t)\) die Atemstromstärke in Litern pro Sekunde. Abbildung 5 zeigt den durch die Funktion \(g\) beschriebenen zeitlichen Verlauf der Atemstromstärke.
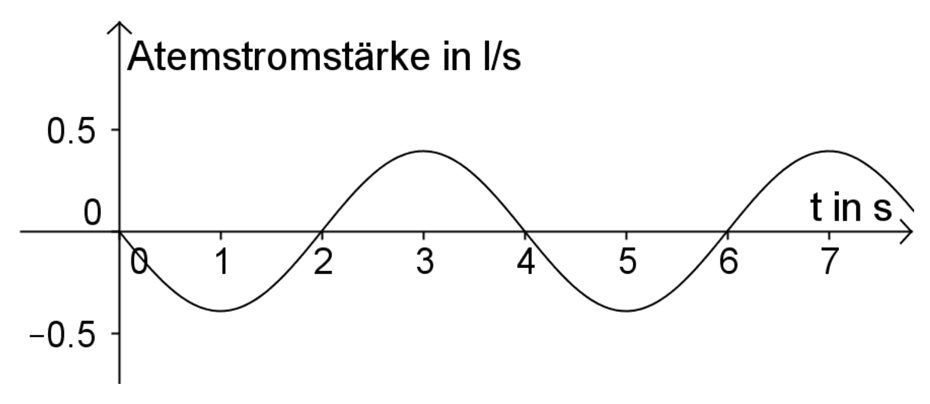
Abb. 5
Berechnen Sie \(g(1{,}5)\) und interpretieren Sie das Vorzeichen dieses Werts im Sachzusammenhang.
(2 BE)
Lösung zu Teilaufgabe 3a
Funktionswert berechnen und im Sachzusammenhang interpretieren
\[g(t) = -\frac{\pi}{8} \sin \left( \frac{\pi}{2}t \right)\,; \enspace D = \mathbb R_{0}^{+}\]
Berechnung von \(g(1{,}5)\)
\[\begin{align*} g(1{,}5) &= -\frac{\pi}{8}\sin\left( \frac{\pi}{2} \cdot 1{,}5 \right) \\[0.8em] &= -\frac{\pi}{8}\sin\left( \frac{3}{4}\pi \right) \\[0.8em] &\approx -0{,}28 \end{align*}\]
Interpretation im Sachzusammenhang
Gemäß der Angabe ist der Wert der Atemstromstärke beim Einatmen positiv. Folglich bedeutet das negative Vorzeichen des Werts, dass die Testperson zum Zeitpunkt \(t = 1{,}5\) Sekunden nach Beobachtungsbeginn ausatmet.

