Für eine Aufgabe aus dem Fachgebiet Mathematik kommen zwei Kuverts zum Einsatz, die jeweils fünf Spielkarten enthalten. Es ist bekannt, dass das eine Kuvert genau zwei und das andere genau drei rote Spielkarten enthält. Der Showmaster wählt, jeweils zufällig, ein Kuvert und aus diesem zwei Karten aus.
Bestätigen Sie rechnerisch, dass die Wahrscheinlichkeit dafür, dass die beiden ausgewählten Karten rot sind, 20 % beträgt.
(4 BE)
Lösung zu Teilaufgabe 3e
1. Lösungsansatz: Auffassung als 3-stufiges Zufallsexperiment
Der Showmaster wählt, jeweils zufällig, ein Kuvert und aus diesem nacheinander zwei Karten aus.
Kuvert A: 2 rote Karten von 5 Spielkarten
Kuvert B: 3 rote Karten von 5 Spielkarten
Baumdiagramm:
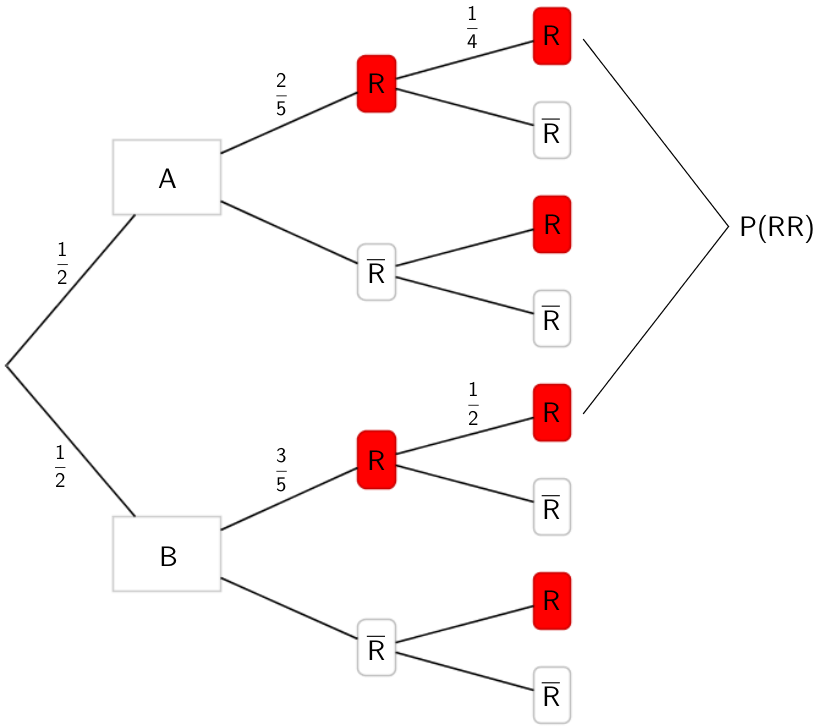
Ziehen ohne Zurücklegen: Das Ziehen einer ersten roten Karte verändert die Wahrscheinlichkeit, eine zweite rote Karte zu ziehen.
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Anwenden der 1. Pfadregel:
\[P(RR \cap A) = \frac{1}{2} \cdot \frac{2}{5} \cdot \frac{1}{4}\]
\[P(RR \cap B) = \frac{1}{2} \cdot \frac{3}{5} \cdot \frac{1}{2}\]
Anwenden der 2. Pfadregel:
\[\begin{align*}P(RR) &= P(RR \cap A) + P(RR \cap B) \\[0.8em] \\[0.8em] &= \frac{1}{2} \cdot \frac{2}{5} \cdot \frac{1}{4} + \frac{1}{2} \cdot \frac{3}{5} \cdot \frac{1}{2} \\[0.8em] &= \frac{1}{20} + \frac{3}{20} \\[0.8em] &= \frac{1}{5} = 20\,\%\end{align*}\]
2. Lösungsansatz: Auffassung als 2-stufiges Zufallsexperiment
Der Showmaster wählt, jeweils zufällig, ein Kuvert und aus diesem "mit einem Griff" zwei Karten aus.
Kuvert A: 2 rote Karten von 5 Spielkarten
Kuvert B: 3 rote Karten von 5 Spielkarten
Baumdiagramm:
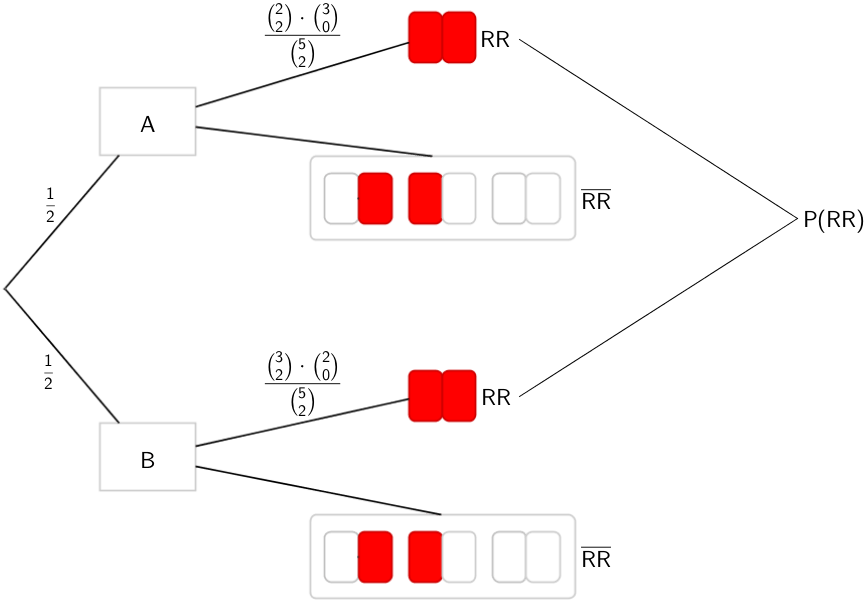
Ziehen ohne Zurücklegen: Die Wahl zweier Karten aus einem Kuvert lässt sich durch das Ziehen mit einem Griff simulieren.
Urnenmodell: „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge"
Werden aus einer Urne mit \(N\) Kugeln, von denen \(K\) Kugeln schwarz sind, \(n\) Kugeln mit einem Griff, d.h. ohne Zurücklegen und ohne Beachtung der Reihenfolge gezogen, so gilt für die Wahrscheinlichkeit, genau \(k\) schwarze Kugeln zu ziehen:
\[P(\text{„genau}\,k\,\text{schwarze Kugeln"}) = \frac{\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}}{\displaystyle \binom{N}{n}}\]
\[P(RR\;\text{aus Kuvert}\;A) = \frac{\displaystyle \binom{2}{2} \cdot \binom{3}{0}}{\displaystyle \binom{5}{2}} = \frac{1 \cdot 1}{10} = \frac{1}{10}\]
\[P(RR\;\text{aus Kuvert}\;B) = \frac{\displaystyle \binom{3}{2} \cdot \binom{2}{0}}{\displaystyle \binom{5}{2}} = \frac{3 \cdot 1}{10} = \frac{3}{10}\]
Anwenden der 1. Pfadregel:
\[P(RR \cap A) = \frac{1}{2} \cdot \frac{1}{10} = \frac{1}{20}\]
\[P(RR \cap B) = \frac{1}{2} \cdot \frac{3}{10} = \frac{3}{20}\]
Anwenden der 2. Pfadregel:
\[\begin{align*}P(RR) &= P(RR \cap A) + P(RR \cap B) \\[0.8em] \\[0.8em] &= \frac{1}{20} + \frac{3}{20} \\[0.8em] &= \frac{1}{5} = 20\,\%\end{align*}\]


