Die Ebene \(E\) teilt den Quader in zwei Teilkörper. Bestimmen Sie den Anteil des Volumens des pyramidenförmigen Teilkörpers am Volumen des Quaders, ohne die Volumina zu berechnen.
(3 BE)
Lösung zu Teilaufgabe e
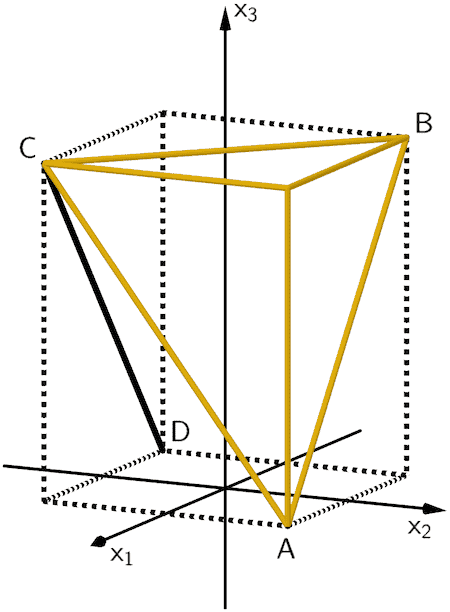
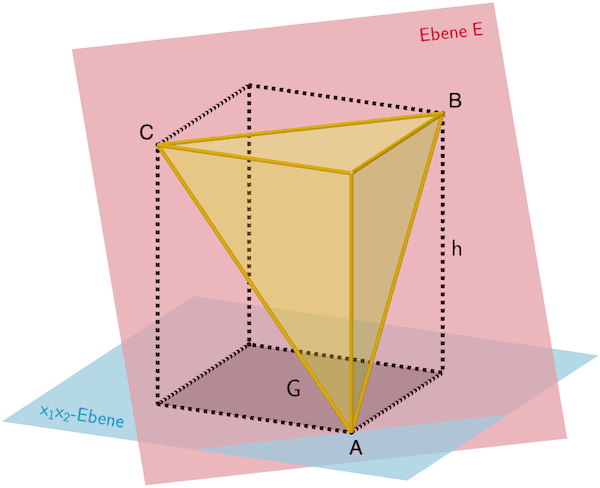
Veranschaulichung des pyramidenförmigen Teilkörpers in Abbildung 2 (optional) sowie ergänzende Darstellung.
Die Höhe der Pyramide ist gleich der Höhe des Quaders. Die Grundfläche der Pyramide ist halb so groß wie die des Quaders.
Volumen einer Pyramide
\[V = \frac{1}{3} \cdot G \cdot h\]
\(G\): Flächeninhalt der Grundfläche der Pyramide
\(h\): Höhe der Pyramide
(vgl. Merkhilfe)
\[\frac{\textcolor{#e9b509}{V_{\text{Pyramide}}}}{V_{\text{Quader}}} = \frac{\frac{1}{3} \cdot \textcolor{#e9b509}{\frac{1}{2} \cdot G} \cdot h}{G \cdot h} = \frac{1}{6}\]

