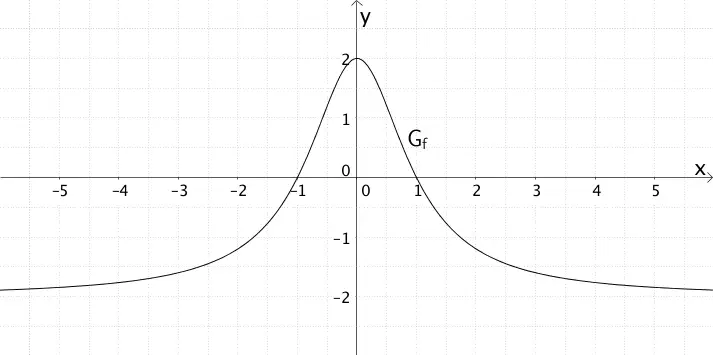
Die Abbildung zeigt den Graphen \(G_{f}\) einer in \(R\) definierten Funktion \(f\).
a) Skizzieren Sie den Graphen \(G_{F}\) der Integralfunktion \(F \colon x \mapsto \displaystyle \int_{0}^{x} f(t) dt\) in die Abbildung. Gehen Sie dabei insbesondere auf die Nullstellen und die Extremstelle von \(G_{f}\) sowie auf das Verhalten von \(G_{f}\) für \(x \to \pm \infty\) ein. Erläutern Sie Ihre Vorgehensweise.
b) „Jede Stammfunktion der abgebildeten Funktion \(f\) ist eine Integralfunktion." Nehmen Sie zu dieser Aussage begründend Stellung, indem Sie sich auf \(G_{F}\) beziehen.
a) Skizzieren des Graphen der Integralfunktion \(F\)
\[F(x) = \int_{0}^{x} f(t) dt\]
Nach dem Hauptsatz der Differential- und Integralrechnung ist die zu skizzierende Integralfunktion \(F\) eine Stammfunktion der Funktion \(f\) und es gilt:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[F'(x) = f(x)\]
Der abgebildete Graph \(G_{f}\) beschreibt demnach den Verlauf des Graphen der Ableitung der zu skizzierenden Integralfunktion \(F\).
Betrachtung der Nullstellen von \(G_{f}\)
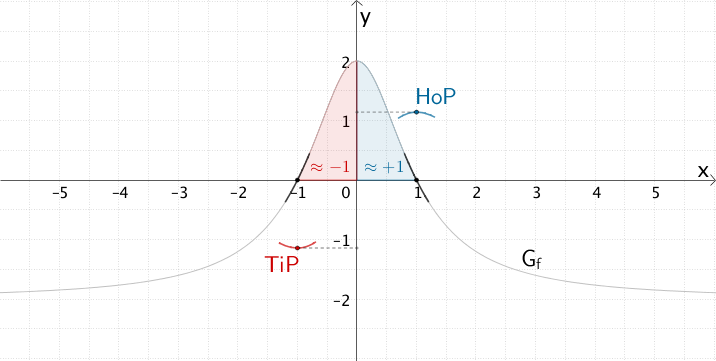
Der Verlauf von \(G_{f}\) zeigt, dass die Funktion \(f\) die einfache Nullstelle \(x = -1\) mit Vorzeichenwechsel von \(-\) nach \(+\) und die einfache Nullstelle \(x = 1\) mit Vorzeichenwechsel von \(x\) nach \(-\) hat.
Mit \(F'(x) = f(x)\) folgt daraus, dass der Graph der Integralfunktion \(F\) an der Stelle \(x = -1\) den Tiefpunkt \(TiP(-1|F(-1))\) und an der Stelle \(x = 1\) den Hochpunkt \(HoP(1|F(1))\) besitzt.
Die \(y\)-Koordinate des Tief- bzw. Hochpunkts lässt sich abschätzen, indem man die Flächenstücke betrachtet, welche \(G_{f}\) im Intervall \([-1;0]\) bzw. \([0;1]\) mit der \(x\)-Achse einschließt. Die Flächeninhalte der Flächenstücke beanspruchen näherungsweise etwas mehr als vier Kästchen und betragen damit etwas mehr als 1 FE (1 Kästchen entspricht 0,25 Flächeneinheiten).
Da im Falle \(\displaystyle F(-1) = \int_{0}^{-1} f(t) dt\) „nach links" integriert wird, zählt der Flächeninhalt des Flächenstücks im Intervall \([-1;0]\) negativ (vgl. Abiturskript - 1.6.3 Bestimmtes Integral, Integrationsregeln, Vertauschungsregel).
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[\left. \begin{align*} &F'(x) < 0 \; \text{für} \; x < -1 \\[0.8em] &F'(-1) = 0 \\[0.8em] &F'(x) > 0 \; \text{für} \; x > -1 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}\; TiP(-1|F(-1))\]
\[\left. \begin{align*} &F'(x) > 0 \; \text{für} \; x < 1 \\[0.8em] &F'(1) = 0 \\[0.8em] &F'(x) < 0 \; \text{für} \; x > 1 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}\; HoP(1|F(1))\]
\[F(-1) = \int_{0}^{-1} f(t) dt = -\int_{-1}^{0} f(t) dt \approx -(4 \cdot 0{,}25) \approx - 1\]
\[F(1) = \int _{0}^{1} f(t) dt \approx 4 \cdot 0{,}25 \approx 1\]
Betrachtung der Extremstelle von \(G_{f}\)
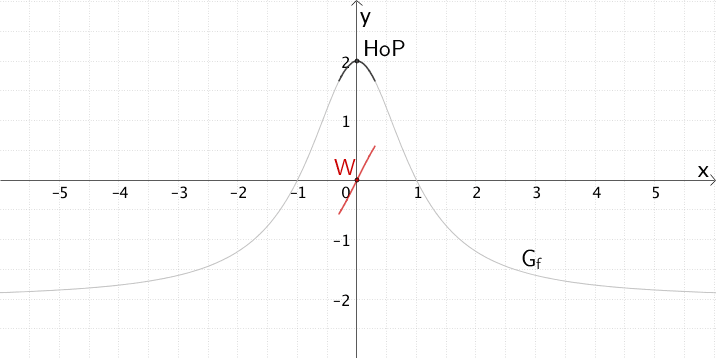
An der Stelle \(x = 0\) besitzt \(G_{f}\) einen Hochpunkt. In der Umgebung des Hochpunkts wechselt der Graph \(G_{f}\) das Monotonieverhalten von „streng monoton steigend" nach „streng monoton fallend".
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\text{Hochpunkt}\; HoP(0|f(0)) \enspace \Rightarrow \enspace \left\{ \begin{align*} &f'(x) > 0 \; \text{für} \; x < 0 \\[0.8em] &f'(0) = 0 \\[0.8em] &f'(x) < 0 \; \text{für} \; x > 0 \end{align*} \right.\]
Mit \(F''(x) = f'(x)\) folgt, dass der Graph der Integralfunktion \(F\) an der Stelle \(x = 0\) den Wendepunkt \(W(0|F(0))\) hat und dort das Krümmungsverhalten von „linksgekrümmt" nach „rechtsgekrümmt" wechselt.
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
\[\left. \begin{align*} &F''(x) > 0 \; \text{für} \; x < 0 \\[0.8em] &F''(0) = 0 \\[0.8em] &F''(x) < 0 \; \text{für} \; x > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkt}\; W(0|F(0))\]
Da jede Integralfunktion an der unteren Integrationsgrenze eine Nullstelle hat, liegt der Wendepunkt \(W(0|f(0))\) mit \(F(0) = 0\) im Koordinatenursprung.
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
\[F(0) = \int_{0}^{0} f(t) dt = 0 \quad \Longrightarrow \quad W(0|0)\]
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
Der Graph \(G_{F}\) der Integralfunktion \(F\) ist
- mit \(F''(x) > 0\) für \(x < 0\) im Intervall \(]-\infty;0[\) linksgekrümmt und
- mit \(F''(x) < 0\) für \(x > 0\) im Intervall \(]0;+\infty[\) rechtsgekrümmt.
Die bereits ermittelten Extrempunkte \(TiP(-1|F(-1))\) und \(HoP(1|F(1))\) (vgl. Betrachtung der Nullstellen von \(G_{f}\)) bestätigen das Krümmungsverhalten von \(G_{F}\).
Betrachtung des Verhaltens von \(G_{f}\) für \(x \to \pm \infty\)
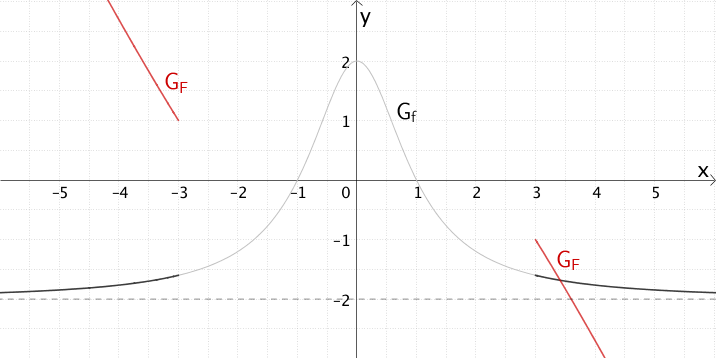
Für \(x \to \pm \infty\) nähert sich der Graph \(G_{f}\) der waagrechten Asymptote mit der Gleichung \(y = -2\) an.
Das heißt, es gilt:
\[\lim \limits_{x \,\to\,\pm\infty} f(x) = -2\]
Mit \(F'(x) = f(x)\) folgt:
\[\lim \limits_{x \,\to\,\pm\infty} F'(x) = -2\]
Die erste Ableitung \(F'(x)\) beschreibt die Steigung einer Tangente an den Graphen der Integralfunktion \(F\).
Die Steigung einer Tangente an \(G_{F}\) ist also für \(x \to \pm \infty\) mit \(m = -2\) näherungsweise konstant. Das bedeutet, dass \(G_{F}\) für \(x \to \pm \infty\) näherungsweise dem Verlauf einer Geraden mit der Steigung \(-2\) folgt.
Zusammenfassung der Ergebnisse
Eigenschaften des Graphen \(G_{F}\) der Integralfunktion \(F\):
- \(G_{F}\) besitzt näherungsweise den Tiefpunkt \(TiP(-1|-1)\) und den Hochpunkt \(HoP(1|1)\).
- \(G_{F}\) verläuft durch den Wendepunkt \(W(0|0)\).
- \(G_{f}\) ist für \(x < 0\) linksgekrümmt und für \(x > 0\) rechtsgekrümmt.
- Für \(x \to \pm \infty\) nähert sich \(G_{F}\) einer Geraden mit der Steigung \(-2\) an.
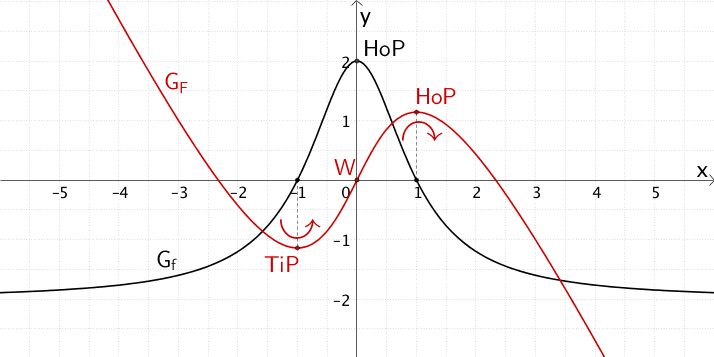
Graph \(G_{f}\) einer in \(\mathbb R\) definierten Funktion \(f\) und Graph \(G_{F}\) der Integralfunktion \(\displaystyle F \colon x \mapsto \int_{0}^{x} f(t) dt\)
b) Bewertung der Aussage „Jede Stammfunktion der abgebildeten Funktion \(f\) ist eine Integralfunktion." unter Bezugnahme auf \(G_{F}\)
(vgl. Abiturskript - 1.6.6 Integralfunktion, Zusammenhang Integralfunktion - Stammfunktion)
Die Aussage ist richtig.
Begründung:
Nach dem Hauptsatz der Differential- und Integralrechnung (HDI) ist jede Integralfunktion \(\displaystyle \int_{a}^{x} f(t) dt\) einer gegebenen stetigen Funktion \(f\) eine Stammfunktion von \(f\).
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Umgekehrt gilt dies nicht, denn jede Integralfunktion hat an der unteren Integrationsgrenze eine Nullstelle, aber nicht jede Stammfunktion muss zwingend eine Nullstelle haben, So kann der Graph einer Stammfunktion ausschließlich oberhalb oder unterhalb der \(x\)-Achse verlaufen, ohne die \(x\)-Achse zu schneiden.
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
Im Falle der abgebildeten Funktion \(f\) hat aber tatsächlich jede Stammfunktion von \(f\) eine Nullstelle. Dies lässt der Graph \(G_{F}\) der Integralfunktion \(F\) erkennen.
Die Graphen der Stammfunktionen von \(f\) unterscheiden sich hinsichtlich Ihres Verlaufs nur durch eine Verschiebung in \(y\)-Richtung. Der Graph \(G_{F}\) ist der Graph einer dieser Stammfunktionen. Da \(G_{F}\) für \(x \to -\infty\) bzw. \(x \to +\infty\) nach \(+\infty\) bzw. \(-\infty\) verläuft, hat der Graph einer Stammfunktion, der bezüglich \(G_{F}\) in \(y\)-Richtung verschoben ist, mindestens eine Nullstelle.
Damit ist jede Stammfunktion der abgebildeten Funktion \(f\) auch eine Integralfunktion.

