Zu einem bestimmten Zeitpunkt fallen auf die Knickpyramide Sonnenstrahlen, die im Modell durch parallele Geraden mit dem Richtungsvektor \(\overrightarrow{S_{15}E}\) dargestellt werden. Der Schatten der Spitze der Knickpyramide auf dem horizontalen Boden wird durch den Punkt \(T\) beschrieben. Die Lote durch die Punkte \(E\), \(F\), \(G\), \(H\) und \(S_{15}\) auf die \(x_1x_2\)-Ebene schneiden diese in den Punkten \(E'\), \(F'\), \(G'\), \(H'\) bzw. \(S'\). Diese sind zusammen mit der Grundfläche der Pyramide und dem Punkt \(T\) in Abbildung 3 dargestellt.
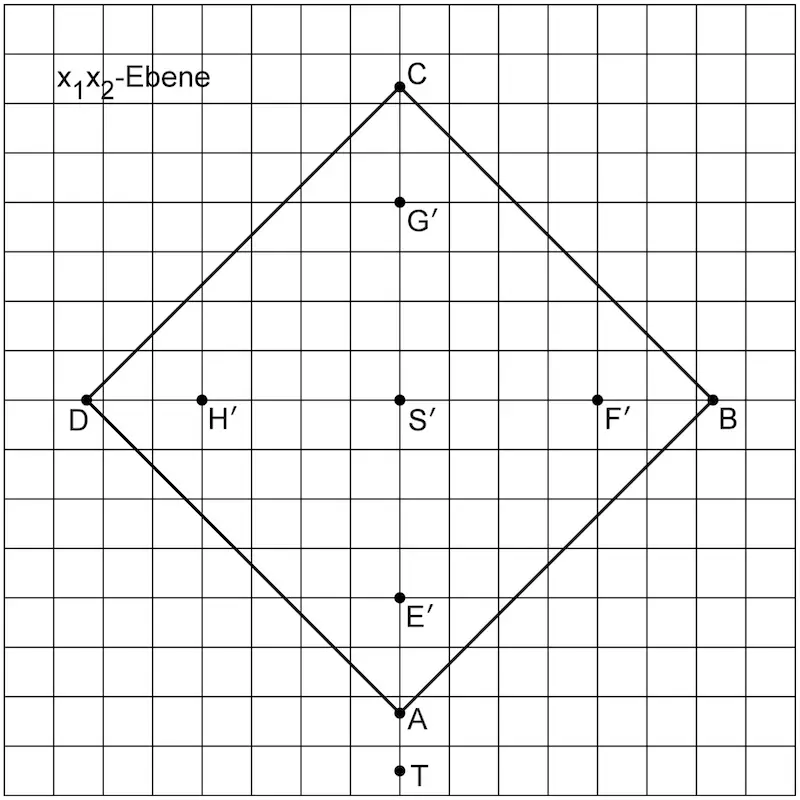Abb. 3
Berechnen Sie die Koordinaten von \(T\).
(3 BE)
Lösung zu Teilaufgabe f
\[S_{15}E \colon \overrightarrow{X} = \begin{pmatrix} 0\\0\\15 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 12\\0\\-8 \end{pmatrix}; \lambda \in \mathbb R\]
\[S_{15}E \cap x_1x_2\text{-Ebene} \colon 15 - 8\lambda = 0 \;\Rightarrow \; \lambda = \frac{15}{8}\]
\[T \in S_{15}E \colon \overrightarrow{T} = \begin{pmatrix} 0\\0\\15 \end{pmatrix} + \frac{15}{8} \cdot \begin{pmatrix} 12\\0\\-8 \end{pmatrix} = \begin{pmatrix} 22{,}5\\0\\0 \end{pmatrix}\]
\[\Rightarrow\;T(22{,}5|0|0)\]
Ausführliche Lösung (nicht verlangt)
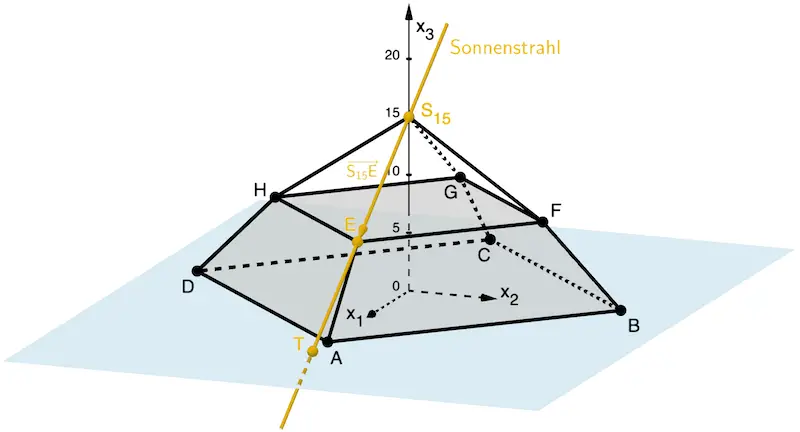
Die Gerade \(\textcolor{#e9b509}{S_{15}E}\) (Sonnenstahl) schneidet die \(\textcolor{#0087c1}{x_1x_2}\)-Ebene im Punkt \(T\).
Gleichung der Gerade \(S_{15}E\) in Parameterform:
Der Vektor \(\textcolor{#e9b509}{\overrightarrow{S_{15}E}}\) ist eine Richtungsvektor der Geradengleichung. Als Aufpunkt wählt man beispielsweise den Punkt \(\textcolor{#e9b509}{S_{15}}\).
\(S_{15}(0|0|15)\), \(E(12|0|7)\)
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\textcolor{#e9b509}{S_{15}E} \colon \overrightarrow{X} = \textcolor{#e9b509}{\overrightarrow{S_{15}}} + \lambda \cdot \textcolor{#e9b509}{\overrightarrow{S_{15}E}}; \lambda \in \mathbb R\]
\[\overrightarrow{S_{15}E} = \overrightarrow{E} - \overrightarrow{S_{15}} = \begin{pmatrix} 12\\0\\7 \end{pmatrix} - \begin{pmatrix} 0\\0\\15 \end{pmatrix} = \begin{pmatrix} 12\\0\\-8 \end{pmatrix}\]
\[S_{15}E \colon \overrightarrow{X} = \begin{pmatrix} 0\\0\\15 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 12\\0\\-8 \end{pmatrix}; \lambda \in \mathbb R\]
Koordinaten von \(T\) berechnen:
\(x_1x_2\text{-Ebene} \colon x_3 = 0\)
\[S_{15}E \colon \overrightarrow{X} = \begin{pmatrix} 0\\0\\15 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 12\\0\\-8 \end{pmatrix} = \begin{pmatrix} 12\lambda\\0\\\textcolor{#cc071e}{15 - 8\lambda} \end{pmatrix}\]
\(\textcolor{#cc071e}{x_3}\)-Koordinate der Geradengleichung in die Gleichung der \(x_1x_2\text{-Ebene}\) einsetzen und die Gleichung nach \(\lambda\) auflösen.
\[\begin{align*}S_{15}E \cap x_1x_2\text{-Ebene} \colon \textcolor{#cc071e}{15 - 8\lambda} &= 0 &&| +8\lambda \\[0.8em] 15 &= 8 \lambda &&| : 8 \\[0.8em] \lambda &= \frac{15}{8} \end{align*}\]
Einsetzen des Parameterwerts \(\textcolor{#89ba17}{\lambda = \dfrac{15}{8}}\) in die Gleichung der Gerade \(S_{15}E\) ergibt den Ortsvektor des Punktes \(T\).
\[T \in S_{15}E \colon \overrightarrow{T} = \begin{pmatrix} 0\\0\\15 \end{pmatrix} + \textcolor{#89ba17}{\frac{15}{8}} \cdot \begin{pmatrix} 12\\0\\-8 \end{pmatrix} = \begin{pmatrix} 22{,}5\\0\\0 \end{pmatrix}\]
\[\Rightarrow\;T(22{,}5|0|0)\]
