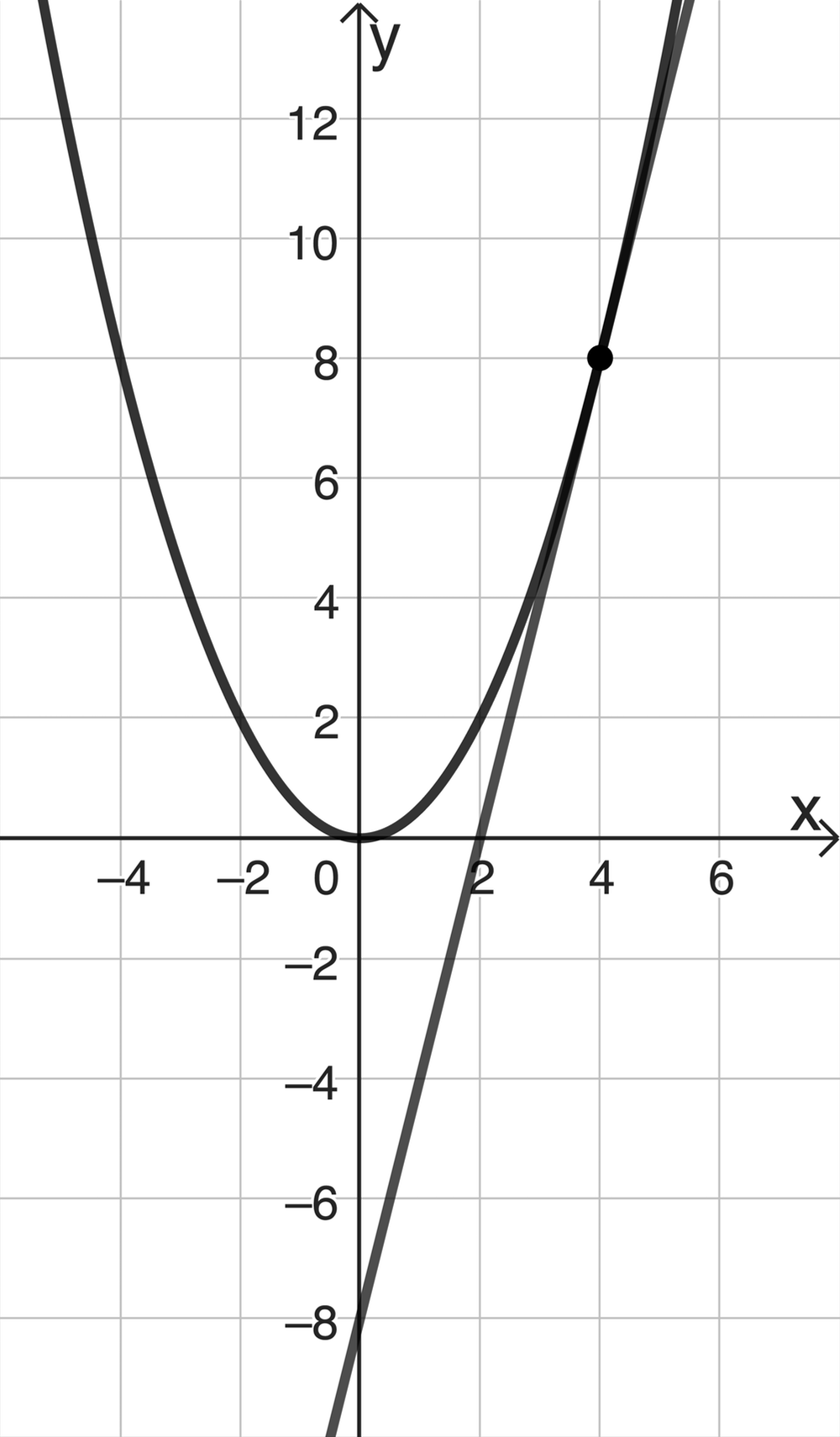
Gegeben ist für jede positive reelle Zahl a die in \(\mathbb R\) definierte Funktion \(f_a\) mit \(f_a(x) = ax^2\). Abbildung 2 zeigt den Graphen von \(f_{\frac{1}{2}}\) sowie die Tangente \(t\) an den Graphen von \(f_{\frac{1}{2}}\) im Punkt \(\big(4 \big| f_{\frac{1}{2}}(4) \big)\).

Geben Sie anhand  von Abbildung 2 eine Gleichung der Tangente \(t\) an.

\[t\colon y = \textcolor{#cc071e}{m}x + \textcolor{#0087c1}{c}\]

Mithilfe eines Steigungsdreiecks und durch Ablesen des \(\textcolor{#0087c1}{y}\)-Achsenabschnitts ergibt sich:

\(\textcolor{#cc071e}{m = \dfrac{\Delta y}{\Delta x} = \dfrac{8}{2} = 4}\) und \(\textcolor{#0087c1}{c = -8}\)

\[\Rightarrow \; t \colon y = \textcolor{#cc071e}{4}x \textcolor{#0087c1}{- 8}\]