Berechnen Sie den Inhalt der Fläche, die der Graph von \(g\) mit der \(x\)-Achse einschließt.
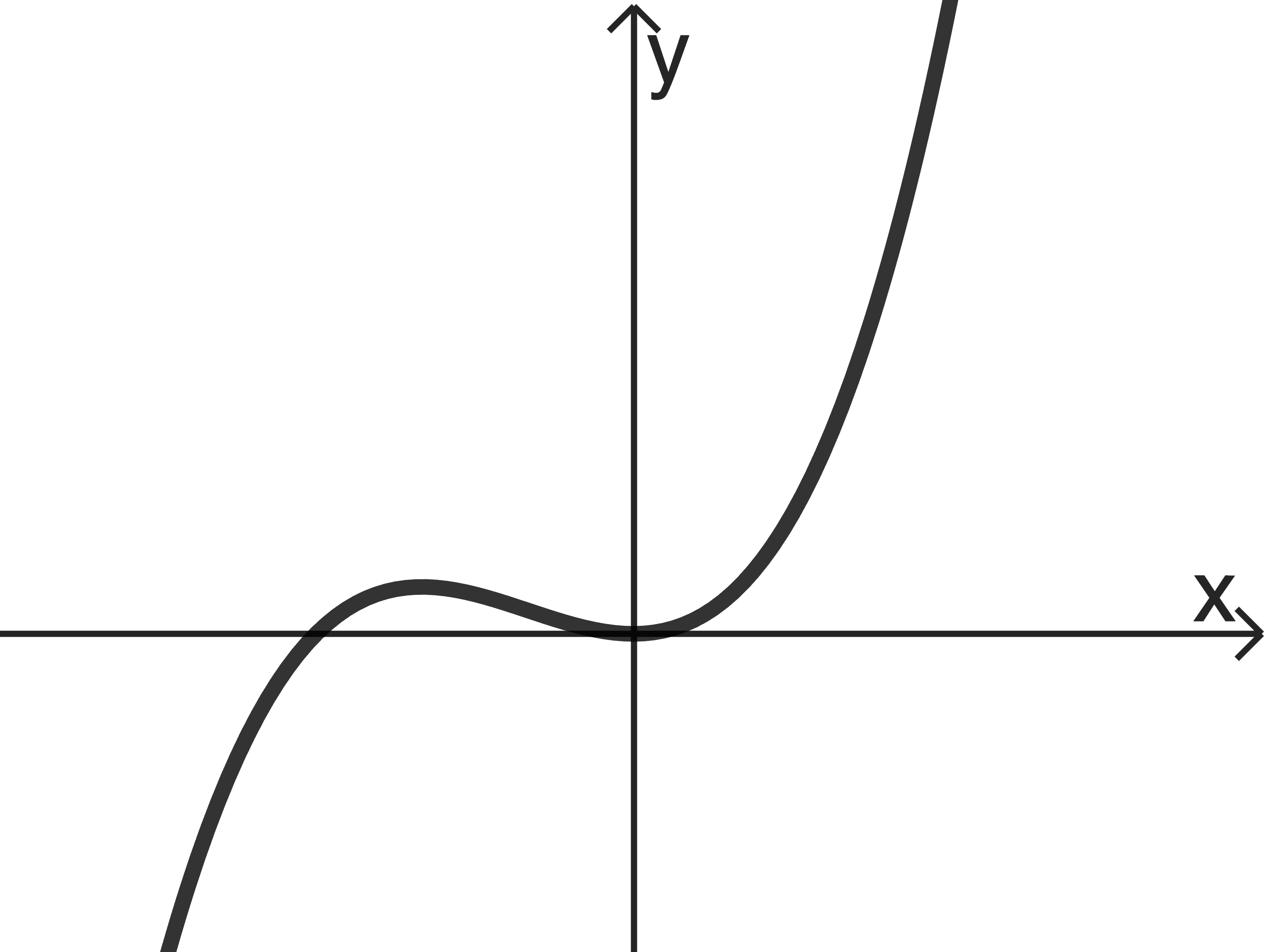Abb. 1
(4 BE)
Lösung zu Teilaufgabe 2b
\[g(x) = x^3+x^2; \;D_g = \mathbb R\]
Der Inhalt der Fläche, die der Graph von \(g\) mit der \(x\)-Achse einschließt, lässt sich durch Integration berechnen.
Zunächst werden die Nullstellen von \(g\) bestimmt. Sie bilden die Integrationsgrenzen.
\[\begin{align*}g(x) &= 0 \\[0.8em] x^3 + x^2 &= 0 &&| \; x^2 \; \text{ausklammern (Produkt formulieren)} \\[0.8em] x^2 \cdot (x+1) &= 0 \end{align*}\]
Somit Nullstellen \(x = -1\) und \(x = 0\)
Flächeninhalt berechnen:
Wichtige unbestimmte Integrale (\(C \in \mathbb R\), vgl. Merkhilfe)
\[\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq - 1)\]
\[\int \frac{1}{x}\,dx = \ln{\vert x \vert} + C\]
\[\int \sin{x} \, dx = -\cos{x} + C\]
\[\int \cos{x} \, dx = \sin{x} + C\]
\[\int e^{x} dx = e^{x} + C\]
\[\int \ln{x}\, dx = -x + x \cdot \ln{x} + C\]
\[\int \frac{f'(x)}{f(x)} dx = \ln{\vert f(x) \vert} + C\]
\[\int f'(x) \cdot e^{f(x)} dx = e^{f(x)} + C\]
\(\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Es gilt die Faktorregel und die Summenregel:
\(\displaystyle \int c \cdot f(x)\,dx = c \cdot \int f(x)\,dx\) mit \(c \in \mathbb R\)
\( \displaystyle \int \left[f(x) \pm g(x) \right] dx = \int f(x)\,dx \pm \int g(x)\,dx\)
\[\begin{align*} \int_{-1}^0 g(x) dx &= \int_{-1}^0 \left( \textcolor{#e9b509}{x^3+x^2} \right)dx &&\Big| \; \int \textcolor{#e9b509}{x^r} dx = \textcolor{#e9b509}{\frac{x^{r + 1}}{r + 1} + C} \;(r \neq -1) \text{(vgl. Merkhilfe)} \\[0.8em] &= \bigg[ \textcolor{#e9b509}{\underbrace{\frac{1}{4}x^4 + \frac{1}{3}x^3}_{\text{Stammfunktion}}} \bigg]_{\textcolor{#0087c1}{-1}}^{\textcolor{#cc071e}{0}} \\[0.8em] &= \frac{1}{4} \cdot \textcolor{#cc071e}{0}^4 + \frac{1}{3} \cdot \textcolor{#cc071e}{0}^3 - \left( \frac{1}{4} \cdot (\textcolor{#0087c1}{-1})^4 + \frac{1}{3} \cdot (\textcolor{#0087c1}{-1})^3 \right) \\[0.8em] &= -\frac{1}{4} + \frac{1}{3} = -\frac{3}{12} + \frac{4}{12} \\[0.8em] &= \frac{1}{12} \end{align*}\]
