Vektoraddition

Gegeben sind die Punkte \(A(2|1|-4)\), \(B(6|1|-12)\) und \(C(0|1|0)\).

Weisen Sie nach, dass der Punkt \(C\) auf der Geraden \(AB\), nicht aber auf der Strecke \([AB]\) liegt.

(3 BE)

Gegeben ist ein Rechteck \(ABCD\) mit den Eckpunkten \(A(5|-4|-3)\), \(B(5|4|3)\), \(C(0|4|3)\) und \(D\).

Ermitteln Sie die Koordinaten von \(D\) und geben Sie die Koordinaten des Mittelpunkts \(M\) der Strecke \([AC]\) an.

(3 BE)

Für jedes \(a \in \mathbb R^{+}\) liegt die Gerade \(g_{a}\) in der Ebene \(U\) mit der Gleichung \(x_{1} = 2{,}5\).

Ein beliebiger Punkt \(P(p_{1}|p_{2}|p_{3})\) des Raums wird an der Ebene \(U\) gespiegelt. Geben Sie die Koordinaten des Bildpunkts \(P'\) in Abhängigkeit von \(p_{1}\), \(p_{2}\) und \(p_{3}\) an.

(2 BE)

Die Strecke \([PQ]\) mit den Eigenschaften \(P(8|-5|1)\) und \(Q\) ist Durchmesser einer Kugel mit Mittelpunkt \(M(5|-1|1)\).

Berechnen Sie die Koordinaten von \(Q\) und weisen Sie nach, dass der Punkt \(R(9|-1|4)\) auf der Kugel liegt.

(3 BE)

Ermitteln Sie die Koordinaten des Eckpunkts \(S\) der Raute \(PQRS\). Zeigen Sie, dass \(PQRS\) kein Quadrat ist.

(2 BE)

Die Punkte \(A(6|0|4)\), \(B(0|6|4)\), \(C(-6|0|4)\) und \(D\) liegen in der Ebene \(E\) und bilden die Eckpunkte der quadratischen Grundfläche einer Pyramide \(ABCDS\) mit der Spitze \(S(0|0|1)\). \(A\), \(B\) und \(S\) liegen in der Ebene \(F\).

Zeigen Sie rechnerisch, dass das Dreieck \(ABS\) gleichschenklig ist. Geben Sie die Koordinaten des Punkts \(D\) an und beschreiben Sie die besondere Lage der Ebene \(E\) im Koordinatensystem.

(4 BE)

Wird der Punkt \(P(1|2|3)\) an der Ebene \(E\) gespiegelt, so ergibt sich der Punkt \(Q(7|2|11)\).

Bestimmen Sie eine Gleichung von \(E\) in Koordinatenform.

(3 BE)

Auf der Gerade durch \(P\) und \(Q\) liegen die Punkte \(R\) und \(S\) symmetrisch bezüglich \(E\); dabei liegt \(R\) bezüglich \(E\) auf der Seite wie \(P\). Der Abstand von \(R\) und \(S\) ist doppelt so groß wie der Abstand von \(P\) und \(Q\).

Bestimmen Sie die Koordinaten von \(R\).

(2 BE)

Bestimmen Sie die Koordinaten zweier Punkte \(C\) und \(D\) so, dass \(C\) auf \(h\) liegt und das Viereck \(ABCD\) eine Raute ist.

(4 BE) 

Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massivem Beton, der die Form eines Spats hat. Alle Seitenflächen eines Spats sind Parallelogramme.

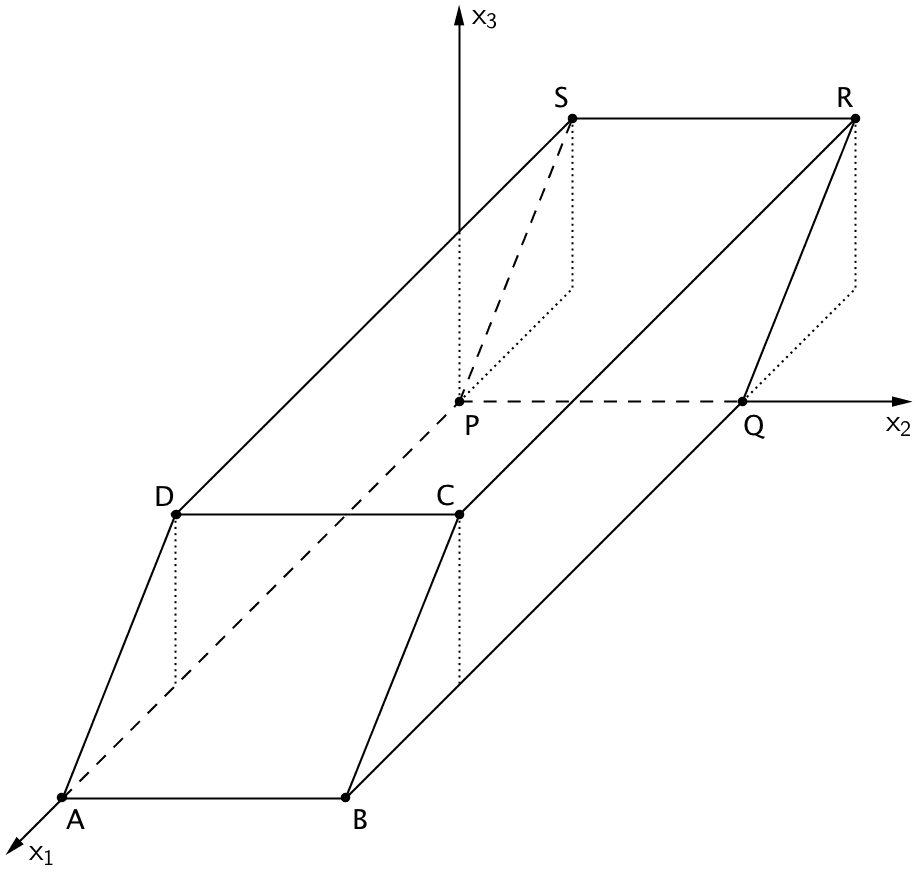
In einem Modell lässt sich der Grundkörper durch einen Spat \(ABCDPQRS\) mit \(A\,(28|0|0)\), \(B\,(28|10|0)\), \(D\,(20|0|6)\) und \(P\,(0|0|0)\) beschreiben (vgl. Abbildung). Die rechteckige Grundfläche \(ABQP\) liegt in der \(x_1x_2\)-Ebene. Im Koordinatensystem entspricht eine Längeneinheit 0,1 m, d.h. der Grundkörper ist 0,6 m hoch.

Geben Sie die Koordinaten des Punkts \(C\) an und zeigen Sie, dass die Seitenfläche \(ABCD\) ein Quadrat ist.

(5 BE)

Die Abbildung zeigt modellhaft einen Austellungspavillon, der die Form einer geraden vierseitigen Pyramide mit quadratischer Grundfläche hat und auf einer horizontalen Fläche steht. Das Dreieck \(BCS\) beschreibt im Modell die südliche Außenwand des Pavillons. Im Koordinatensystem entspricht eine Längeneinheit 1 m, d.h. die Grundfläche des Pavillons hat eine Seitenlänge von 12 m.

Geben Sie die Koordinaten des Punkts \(B\) an und bestimmen Sie das Volumen des Pavillons.

(3 BE)

Geben Sie die Koordinaten zweier Punkte \(P\) und \(Q\) an, die auf \(g\) liegen und von \(T\) gleich weit entfernt sind.

(2 BE)