Analysis 2

Begründen Sie, dass \(F_{1}\) höchstens vier Nullstellen hat.

(2 BE)

Für \(0 \leq x \leq 5\) gilt, dass der Graph von \(f\) und der Graph einer trigonometrischen Funktion \(h\)

●  die gleichen Schnittpunkte mit der \(x\)-Achse besitzen,

●  beide nicht unterhalb der \(x\)-Achse verlaufen,

●  jeweils mit der \(x\)-Achse eine Fläche des Inhalts \(\frac{625}{72}\) einschließen.

Bestimmen Sie einen Term einer solchen Funktion \(h\).

(6 BE)

Die Kosten, die einem Unternehmen bei der Herstellung einer Flüssigkeit entstehen, können durch die Funktion \(K \colon x \mapsto x^{3} - 12x^{2} + 50x + 20\) mit \(x \in [0;9]\) beschrieben werden. Dabei gibt \(K(x)\) die Kosten in 1000 Euro an, die bei der Produktion von \(x\) Kubikmetern der Flüssigkeit insgesamt entstehen. Abbildung 2 zeigt den Graphen von \(K\).

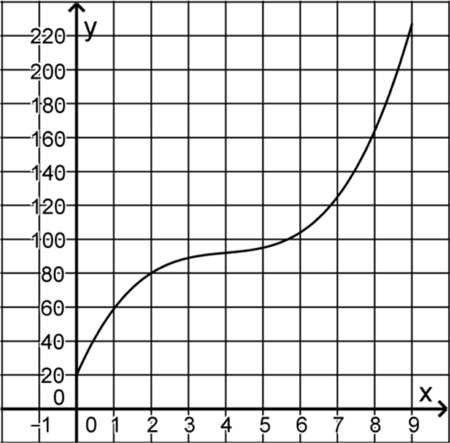Abb. 2

Geben Sie mithilfe von Abbildung 2

α)  die Produktionsmenge an, bei der die Kosten 125 000 Euro betragen.

β)  das Monotonieverhalten von \(K\) an und deuten Sie Ihre Angabe im Sachzusammenhang.

(3 BE)

Die Funktion \(E\) mit \(E(x) = 23x\) gibt für \(0 \leq x \leq 9\) den Erlös (in 1000 Euro) an, den das Unternehmen beim Verkauf von \(x\) Kubikmetern der Flüssigkeit erzielt. Für die sogenannte Gewinnfunktion \(G\) gilt \(G(x) = E(x) - K(x)\). Positive Werte von \(G\) werden als Gewinn bezeichnet, negative als Verlust.

Zeigen Sie, dass das Unternehmen keinen Gewinn erzielt, wenn vier Kubikmeter der Flüssigkeit verkauft werden.

(2 BE)

Zeichnen Sie den Graphen von \(E\) in Abbildung 2 ein. Bestimmen Sie mithilfe der so entstehenden Darstellung den Bereich, in dem die verkaufte Menge der Flüssigkeit liegen muss, damit das Unternehmen einen Gewinn erzielt.

(3 BE)

Berechnen Sie, welche Menge der Flüssigkeit verkauft werden muss, damit das Unternehmen den größten Gewinn erzielt.

(5 BE)

Gegeben ist die Funktion \(g \colon x \mapsto \sqrt{x + 1} - 2\) mit maximaler Definitionsmenge \(D\).

Geben Sie \(D\) an.

(1 BE)

Bestimmen Sie die Gleichung der Tangente an den Graphen von \(g\) im Punkt \((8|g(8))\).

(4 BE)

Gegeben ist die in \(\mathbb R \backslash \{0\}\) definierte Funktion \(f \colon x \mapsto 1 - \dfrac{1}{x^{2}}\), die die Nullstellen \(x_{1} = -1\) und \(x_{2} = 1\) hat. Abbildung 1 zeigt den Graphen von f, der symmetrisch bezüglich der \(y\)-Achse ist. Weiterhin ist die Gerade \(g\) mit der Gleichung \(y = -3\) gegeben.

Abb. 1

Zeigen Sie, dass einer der Punkte, in denen \(g\) den Graphen von \(f\) schneidet, die \(x\)-Koordinate \(\frac{1}{2}\) hat.

(1 BE)

Bestimmen Sie rechnerisch den Inhalt der Fläche, die der Graph von f, die \(x\)-Achse und die Gerade \(g\) einschließen.

(4 BE)

Gegeben ist die Schar der in \(\mathbb R\) definierten Funktionen \(p_{k} \colon x \mapsto kx^{2} - 4x - 3\) mit \(k \in \mathbb R \backslash \{0\}\), deren Graphen Parabeln sind.

Bestimmen Sie den Wert von \(k\) so, dass der Punkt \((2|-3)\) auf der zugehörigen Parabel liegt.

(2 BE)

Ermitteln Sie diejenigen Werte von \(k\), für die die jeweils zugehörige Funktion \(p_{k}\) keine Nullstelle besitzt.

(3 BE)

Die nebenstehende Abbildung 2 zeigt den Graphen einer Funktion \(f\).

Abb. 2

Einer der folgenden Graphen I, II und III gehört zur ersten Ableitungsfunktion von \(f\). Geben Sie diesen an. Begründen Sie, dass die beiden anderen Graphen dafür nicht infrage kommen.

Abb. 3

(3 BE)

Die Funktion \(F\) ist eine Stammfunktion von \(f\). Geben Sie das Monotonieverhalten von \(F\) im Intervall \([1;3]\) an. Begründen Sie Ihre Angabe.

(2 BE)

Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{4x}{(x + 1)^{2}}\) mit Definitionsmenge \(D_{f} = \mathbb R \backslash \{-1\}\). Die Abbildung zeigt den Verlauf des Graphen \(G_{f}\) von \(f\) im I. Quadranten.

Begründen Sie, dass \(x = 0\) die einzige Nullstelle von \(f\) ist. Geben Sie die Gleichung der senkrechten Asymptote von \(G_{f}\) an und begründen Sie anhand des Funktionsterms von \(f\), dass \(G_{f}\) die Gerade mit der Gleichung \(y = 0\) als waagrechte Asymptote besitzt.

(3 BE)

Bestimmen Sie rechnerisch Lage und Art des Extrempunkts von \(G_{f}\).

(5 BE)

Begründen Sie, dass \(G_{f}\) für \(x < 0\) nur im III. Quadranten verläuft, und zeichnen Sie in die Abbildung den darin fehlenden Teil von \(G_{f}\) ein. Berechnen Sie dazu \(f(-3)\) und drei weitere geeignete Funktionswerte von \(f\).

(4 BE)

Gegeben ist ferner die in \(]-1;+\infty[\) definierte Funktion \(F \colon x \mapsto 4 \cdot \ln{(x + 1)} + \dfrac{4}{x + 1}\).

Zeigen Sie, dass \(F\) für \(x > -1\) eine Stammfunktion von \(f\) ist.

(3 BE)

Ein Pharmaunternehmen führt eine Studie zur Wirksamkeit und Verträglichkeit eines neu entwickelten Medikaments durch. Wenn das Medikament einmalig in Form einer Tablette eingenommen wird, kann die zeitliche Entwicklung der Konzentration des Wirkstoffs im Blut des Patienten modellhaft durch die betrachtete Funktion \(f\) für \(x \in [0;9]\) beschrieben werden. Dabei steht \(x\) für die Zeit in Stunden seit der Einnahme der Tablette und \(f(x)\) für die Konzentration des Wirkstoffs im Blut des Patienten (im Weiteren kurz als Wirkstoffkonzentration bezeichnet) in Milligramm pro Liter \(\big( \frac{\sf{mg}}{\sf{l}}\big)\).

Die folgenden Aufgaben e bis i sollen auf der Grundlage dieses Modells bearbeitet werden.

Berechnen Sie die Wirkstoffkonzentration 30 Minuten nach Einnahme der Tablette und geben Sie die maximal auftretende Wirkstoffkonzentration an.

(2 BE)

An der Stelle \(x = 2\) hat \(G_{f}\) einen Wendepunkt. Beschreiben Sie, wie man rechnerisch vorgehen könnte, um dies zu begründen. Geben Sie die Bedeutung der \(x\)-Koordinate des Wendepunkts im Sachzusammenhang an.

(3 BE)