Prüfungsteil B

Für \(0 \leq x \leq 5\) gilt, dass der Graph von \(f\) und der Graph einer trigonometrischen Funktion \(h\)

●  die gleichen Schnittpunkte mit der \(x\)-Achse besitzen,

●  beide nicht unterhalb der \(x\)-Achse verlaufen,

●  jeweils mit der \(x\)-Achse eine Fläche des Inhalts \(\frac{625}{72}\) einschließen.

Bestimmen Sie einen Term einer solchen Funktion \(h\).

(6 BE)

Die Kosten, die einem Unternehmen bei der Herstellung einer Flüssigkeit entstehen, können durch die Funktion \(K \colon x \mapsto x^{3} - 12x^{2} + 50x + 20\) mit \(x \in [0;9]\) beschrieben werden. Dabei gibt \(K(x)\) die Kosten in 1000 Euro an, die bei der Produktion von \(x\) Kubikmetern der Flüssigkeit insgesamt entstehen. Abbildung 2 zeigt den Graphen von \(K\).

Abb. 2

Geben Sie mithilfe von Abbildung 2

α)  die Produktionsmenge an, bei der die Kosten 125 000 Euro betragen.

β)  das Monotonieverhalten von \(K\) an und deuten Sie Ihre Angabe im Sachzusammenhang.

(3 BE)

Die Funktion \(E\) mit \(E(x) = 23x\) gibt für \(0 \leq x \leq 9\) den Erlös (in 1000 Euro) an, den das Unternehmen beim Verkauf von \(x\) Kubikmetern der Flüssigkeit erzielt. Für die sogenannte Gewinnfunktion \(G\) gilt \(G(x) = E(x) - K(x)\). Positive Werte von \(G\) werden als Gewinn bezeichnet, negative als Verlust.

Zeigen Sie, dass das Unternehmen keinen Gewinn erzielt, wenn vier Kubikmeter der Flüssigkeit verkauft werden.

(2 BE)

Begründen Sie ohne Rechnung, dass \(g\) in der \(x_1x_2\)-Ebene liegt.

(1 BE)

Geben Sie für \(a\), \(b\) und \(c\) alle Werte an, sodass sowohl \(D_{a,b,c}  = \mathbb R\) gilt als auch, dass der Graph von \(f_{a,b,c}\) symmetrisch bezüglich des Koordinatenursprungs, aber nicht identisch mit der \(x\)-Achse ist.

(3 BE)

Beim Übergang zwischen den beiden Abschnitten des Bohrkanals muss die Bohrrichtung um den Winkel geändert werden, der im Modell durch den Schnittwinkel der beiden Geraden \(AP\) und \(PQ\) beschrieben wird. Bestimmen Sie die Größe dieses Winkels.

(3 BE)

Die Punkte \(A\), \(B\), \(E\) und \(F\) liegen in der Ebene \(L\). Ermitteln Sie eine Gleichung von \(L\) in Normalenform.

(zur Kontrolle: \(L \colon 2x_{1} + 2x_{2} + 3x_{3} - 12 = 0\))

(4 BE)

Bestimmen Sie unter Verwendung dieser Binomialverteilung die kleinste Geschwindigkeit \(v^{*}\), für die die folgende Aussage zutrifft: „Bei mehr als 95 % der erfassten Fahrten wird \(v^{*}\) nicht überschritten."

(2 BE)

Die Polizei führt an der Messstelle eine Geschwindigkeitskontrolle durch. Bei einer Geschwindigkeit von mehr als 83 km/h liegt ein Tempoverstoß vor. Vereinfachend soll davon ausgegangen werden, dass die Geschwindigkeit eines vorbeifahrenden Pkw mit einer Wahrscheinlichkeit von 19 % größer als 83 km/h ist.

Berechnen Sie die Anzahl der Geschwindigkeitsmessungen, die mindestens durchgeführt werden müssen, damit mit einer Wahrscheinlichkeit von mehr als 99 % mindestens ein Tempoverstoß erfasst wird.

(4 BE)

Liegt in einer Stichprobe von 50 Geschwindigkeitsmessungen die Zahl der Tempoverstöße um mehr als eine Standardabweichung unter dem Erwartungswert, geht die Polizei davon aus, dass wirksam vor der Geschwindigkeitskontrolle gewarnt wurde, und bricht die Kontrolle ab. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Geschwindigkeitskontrolle fortgeführt wird, obwohl die Wahrscheinlichkeit dafür, dass ein Tempoverstoß begangen wird, auf 10 % gesunken ist.

(5 BE)

Ein Unternehmen stellt Kunststoffteile her. Erfahrungsgemäß sind 4 % der hergestellten Teile fehlerhaft. Die Anzahl fehlerhafter Teile unter zufällig ausgewählten kann als binomialverteilt angenommen werden.

50 Kunststoffteile werden zufällig ausgewählt. Bestimmen Sie für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:

\(A\):  „Genau zwei der Teile sind fehlerhaft."

\(B\):  „Mindestens 6 % der Teile sind fehlerhaft."

(3 BE)

Bestimmen Sie eine Gleichung der Ebene \(E\) in Koordinatenform und zeigen Sie, dass die Gerade \(g\) in \(E\) liegt.

(zur Kontrolle: \(E \colon 2x_1 - x_2 + 2x_3 + 35 = 0\))

(5 BE)

Begründen Sie: Wenn \(a = 0\) und \(b \neq 0\) gilt, dann ist der Graph von \(f_{a,b,c}\) symmetrisch bezüglich der \(y\)-Achse und schneidet die \(x\)-Achse nicht. 

(2 BE)

Eine Geothermieanlage fördert durch einen Bohrkanal heißes Wasser aus einer wasserführenden Gesteinsschicht an die Erdoberfläche. In einem Modell entspricht die \(x_{1}x_{2}\)-Ebene eines kartesischen Koordinatensystems der horizontal verlaufenden Erdoberfläche. Eine Längeneinheit im Koordinatensystem entspricht einem Kilometer in der Realität. Der Bohrkanal besteht aus zwei Abschnitten, die im Modell vereinfacht durch die Strecken \([AP]\) und \([PQ]\) mit den Punkten \(A(0|0|0)\), \(P(0|0|-1)\) und \(Q(1|1|-3{,}5)\) beschrieben werden (vgl. Abbildung).

Berechnen Sie auf der Grundlage des Modells die Gesamtlänge des Bohrkanals auf Meter gerundet.

(2 BE)

Der Angestellte konnte bei der Durchführung des Tests zehn von 100 erwachsenen Besuchern dazu animieren, Lose zu kaufen. Er behauptet, dass er zumindest bei Personen mit Kind eine Erfolgsquote größer als 10 % habe. Unter den 100 angesprochenen Besuchern befanden sich 40 Personen mit Kind. Von den Personen ohne Kind zogen 54 kein Los. Überprüfen Sie, ob das Ergebnis der Stichprobe die Behauptung des Angestellten stützt.

(2 BE)

Die Größen der Sektoren werden geändert. Dabei werden der grüne und der rote Sektor verkleinert, wobei der Mittelpunktswinkel des roten Sektors wieder doppelt so groß wie der des grünen Sektors ist. Die Abbildung zeigt einen Teil eines Baumdiagramms, das für das geänderte Glücksrad die beiden ersten Drehungen beschreibt. Ergänzend ist für einen Pfad die zugehörige Wahrscheinlichkeit angegeben.

Bestimmen Sie die Größe des zum grünen Sektor gehörenden Mittelpunktswinkels.

(5 BE)

Auf einem Spielplatz wird ein dreieckiges Sonnensegel errichtet, um einen Sandkasten zu beschatten. Hierzu werden an drei Ecken des Sandkastens Metallstangen im Boden befestigt, an deren Enden das Sonnensegel fixiert wird.

In einem kartesischen Koordinatensystem stellt die \(x_{1}x_{2}\)-Ebene den horizontalen Boden dar. Der Sandkasten wird durch das Rechteck mit den Eckpunkten \(K_{1}(0|4|0)\), \(K_{2}(0|0|0)\), \(K_{3}(3|0|0)\) und \(K_{4}(3|4|0)\) beschrieben. Das Sonnensegel wird durch das ebene Dreieck mit den Eckpunkten \(S_{1}(0|6|2{,}5)\), \(S_{2}(0|0|3)\) und \(S_{3}(6|0|2{,}5)\) dargestellt (vgl. Abbildung 1). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.

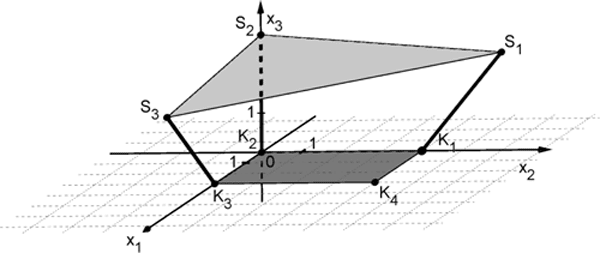Abb. 1

Die Punkte \(S_{1}\), \(S_{2}\) und \(S_{3}\) legen die Ebene \(E\) fest.

Ermitteln Sie eine Gleichung der Ebene \(E\) in Normalenform.

(zur Kontrolle: \(E \colon x_{1} + x_{2} + 12x_{3} - 36 = 0\))

(4 BE)

Der Hersteller des Sonnensegels empfiehlt, die verwendeten Metallstangen bei einer Sonnensegelfläche von mehr als 20 m² durch zusätzliche Sicherungsseile zu stabilisieren. Beurteilen Sie, ob eine solche Sicherung aufgrund dieser Empfehlung in der vorliegenden Situation nötig ist

(3 BE)

Auf das Sonnensegel fallen Sonnenstrahlen, die im Modell und in der Abbildung 1 durch parallele Geraden mit dem Richtungsvektor \(\overrightarrow{S_{1}K_{1}}\) dargestellt werden können. Das Sonnensegel erzeugt auf dem Boden einen dreieckigen Schatten. Die Schatten der mit \(S_{2}\) bzw. \(S_{3}\) bezeichneten Ecken des Sonnensegels werden mit \({S_{2}}'\) bzw. \(S_{3}'\) bezeichnet.

Begründen Sie ohne weitere Rechnung, dass \({S_{2}}'\) auf der \(x_{2}\)-Achse liegt.

(2 BE)

Gegeben sind die Punkte \(P(4|5|-19)\), \(Q(5|9|-18)\) und \(R(3|7|-17)\), die in der Ebene \(E\) liegen, sowie die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} -12 \\ 11 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix}, \; \lambda \in \mathbb R\).

Bestimmen Sie die Länge der Strecke \([PQ]\). Zeigen Sie, dass das Dreieck \(PQR\) bei \(R\) rechtwinklig ist, und begründen Sie damit, dass die Strecke \([PQ]\) Durchmesser des Umkreises des Dreiecks \(PQR\) ist.

(zur Kontrolle: \(\overline{PQ} = 3\sqrt{2}\))

(4 BE)