Die Abbildung 1 zeigt das sogenannte Saarpolygon, ein im Inneren begehbares Denkmal zur Erinnerung an den stillgelegten Kohlebergbau im Saarland. Das Saarpolygon kann in einem Koordinatensystem modellhaft durch den Streckenzug dargestellt werden, der aus den drei Strecken \([AB]\), \([BC]\) und \([CD]\) mit \(A(11|11|0)\), \(B(-11|11|28)\), \(C(11|-11|28)\) und \(D(-11|-11|0)\) besteht (vgl. Abbildung 2). \(A\), \(B\), \(C\) und \(D\) sind Eckpunkte eines Quaders. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.
 Abb. 1
Abb. 1
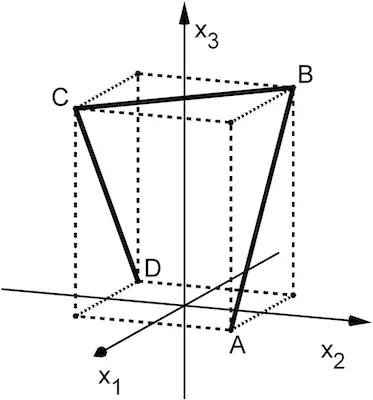 Abb. 2
Abb. 2
Begründen Sie, dass die Punkte \(B\) und \(C\) symmetrisch bezüglich der \(x_3\)-Achse liegen.
(2 BE)