- Details
- Kategorie: Geometrie 1
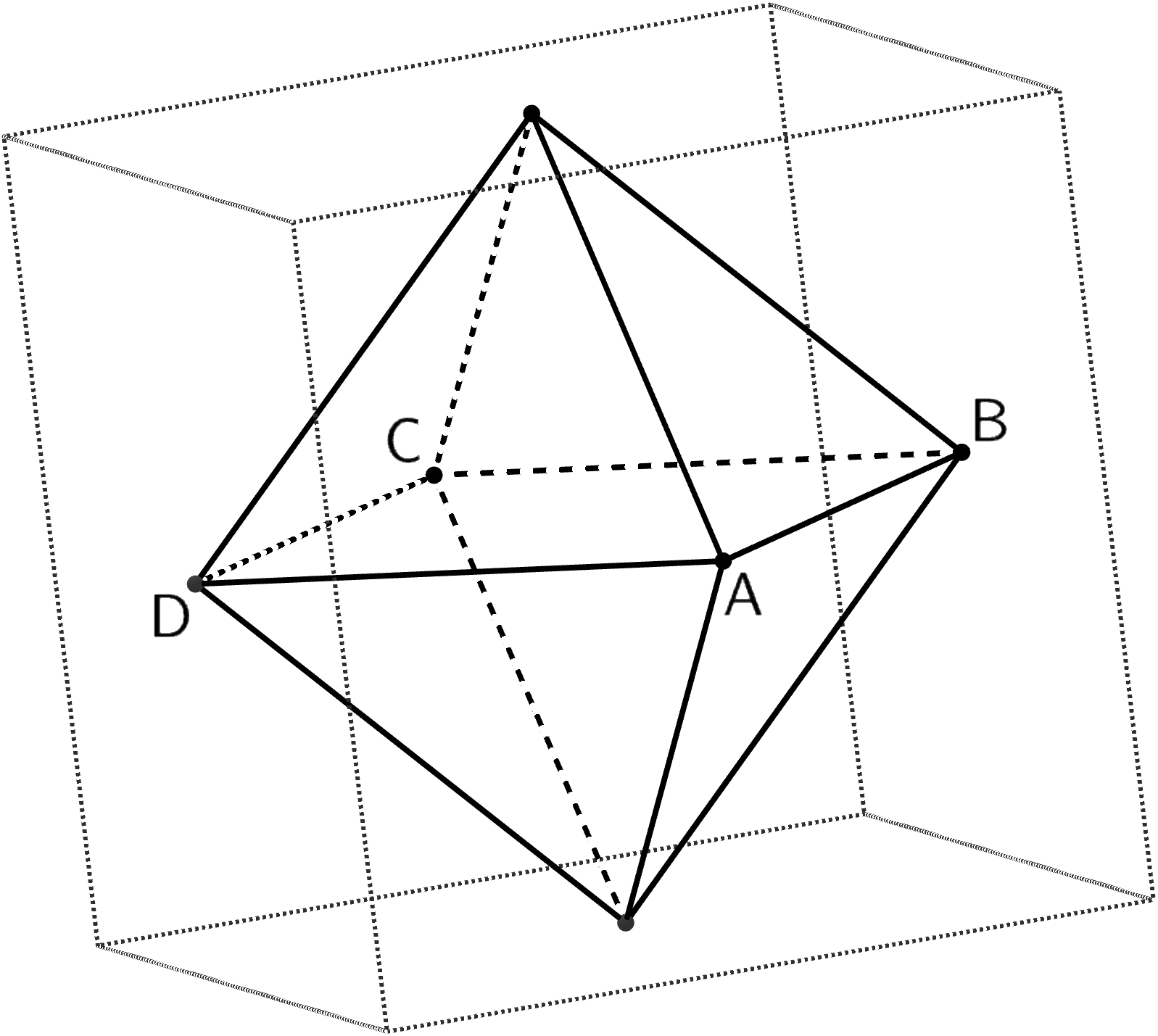
Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung). Die Eckpunkte \(A(1|2|1)\), \(B\), \(C(-3|-6|9)\) und \(D\) des Oktaeders liegen in der Ebene \(H\) mit der Gleichung \(2x_1 + x_2 + 2x_3 - 6 = 0\).
Weisen Sie nach, dass die Kantenlänge des Würfels 12 beträgt.
(2 BE)
- Details
- Kategorie: Geometrie 1
Bestimmen Sie die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in \(H\) liegen.
(3 BE)


