- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto 8x^3+3x\) mit der Ableitungsfunktion \(f'\).
Berechnen Sie \(f'(1)\).
(2 BE)
- Details
- Kategorie: Analysis 1
Bestimmen Sie einen Term derjenigen Stammfunktion \(F\) von \(f\), deren Graph durch den Punkt \((-1|5)\) verläuft.
(3 BE)
- Details
- Kategorie: Analysis 1
Die Abbildung zeigt den Graphen \(G_g\) der in \(\mathbb R\) definierten Funktion \(g\) mit \(g(x) = 2 \cdot \sin{\left( \dfrac{1}{2}x \right)}\).
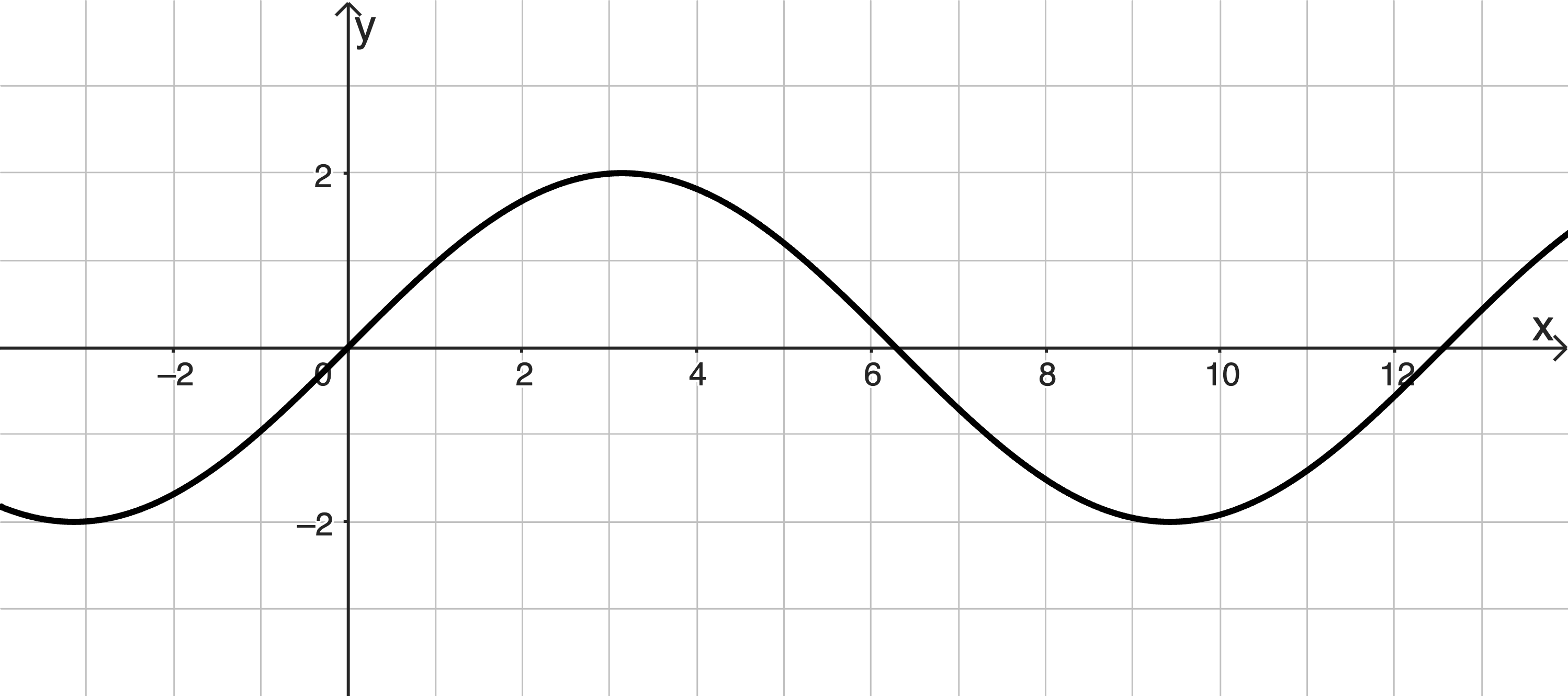
Beurteilen Sie mithilfe der Abbildung, ob der Wert des Integrals \(\displaystyle \int_{-2}^8 g(x)dx\) negativ ist.
(2 BE)
- Details
- Kategorie: Analysis 1
Weißen Sie rechnerisch nach, dass die folgende Aussage zutrifft:
Die Tangente an \(G_g\) im Koordinatenursprung ist die Gerade durch die Punkte \((\textit{-1}|\textit{-1})\) und \((\textit{1}|\textit{1})\).
(3 BE)
- Details
- Kategorie: Analysis 1
Betrachtet wird die Schar der in \(\mathbb R\) definierten Funktionen \(f_a\) mit \(f_a(x) = x \cdot e^{ax}\) und \(a \in \mathbb R \backslash\{0\}\). Für jeden Wert von \(a\) besitzt die Funktion \(f_a\) genau eine Extremstelle.
Begründen Sie, dass der Graph von \(f_a\) für \(x<0\) unterhalb der \(x\)-Achse verläuft.
(2 BE)
- Details
- Kategorie: Analysis 1
Die abgebildeten Graphen I und II sind Graphen der Schar; einer der beiden gehört zu einem positiven Wert von \(a\). Entscheiden Sie, welcher Graph dies ist, und begründen Sie Ihre Entscheidung.
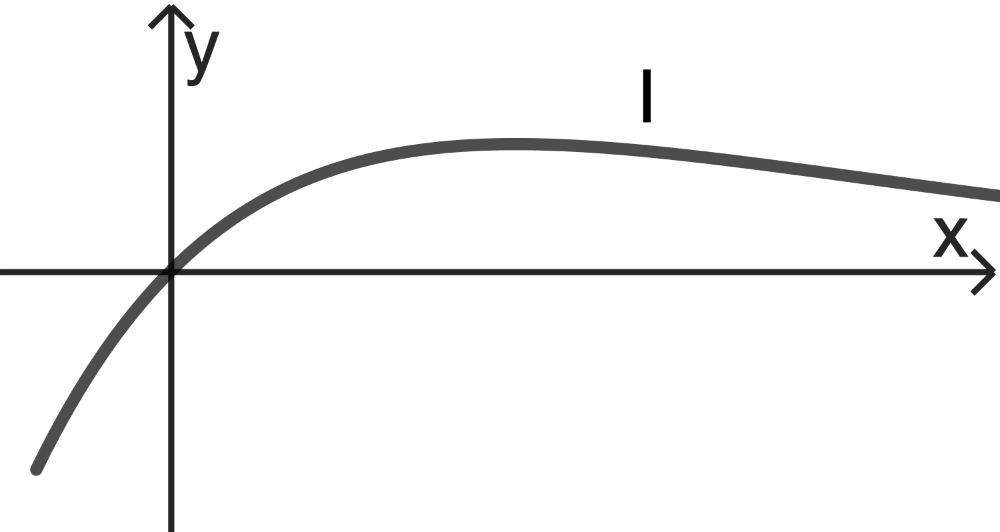
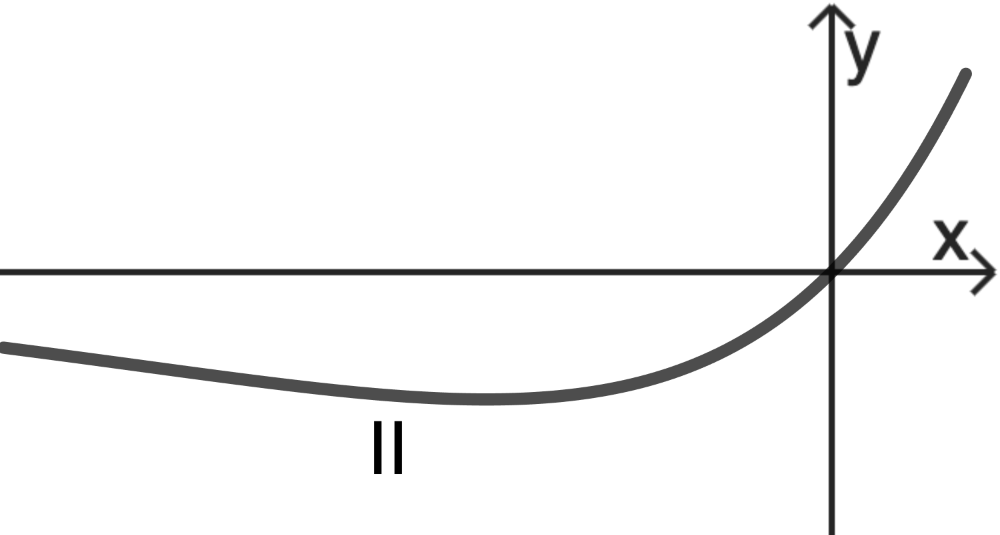
(3 BE)
- Details
- Kategorie: Analysis 1
Geben Sie einen Term einer in \(\mathbb R\) definierten Funktion \(g\) an, die den Wertebereich \([-2;4]\) hat.
(2 BE)
- Details
- Kategorie: Analysis 1
Geben Sie einen Term einer in \(\mathbb R\) definierten Funktion \(h\) an, sodass der Term \(\sqrt{h(x)}\) genau für \(x \in [-2;4]\) definiert ist. Erläutern Sie die Ihrer Angabe zugrunde liegenden Überlegungen.
(3 BE)


