- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R \backslash \{-2\}\) definierte Funktion \(f \colon x \mapsto \dfrac{x^2-9}{x+2}\).
Geben Sie die Nullstellen von \(f\) sowie die Koordinaten des Schnittpunkts des Graphen von \(f\) mit der \(y\)-Achse an.
(2 BE)
- Details
- Kategorie: Analysis 2
Geben Sie das Verhalten für \( x \to -\infty\) sowie für \(x \to +\infty\) an.
(2 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R\) definierte Funktion \(g\) mit \(g(x) = x^3+x^2\). Abbildung 1 zeigt den Graphen von \(g\).
Geben Sie einen Term der ersten Ableitungsfunktion von \(g\) an.
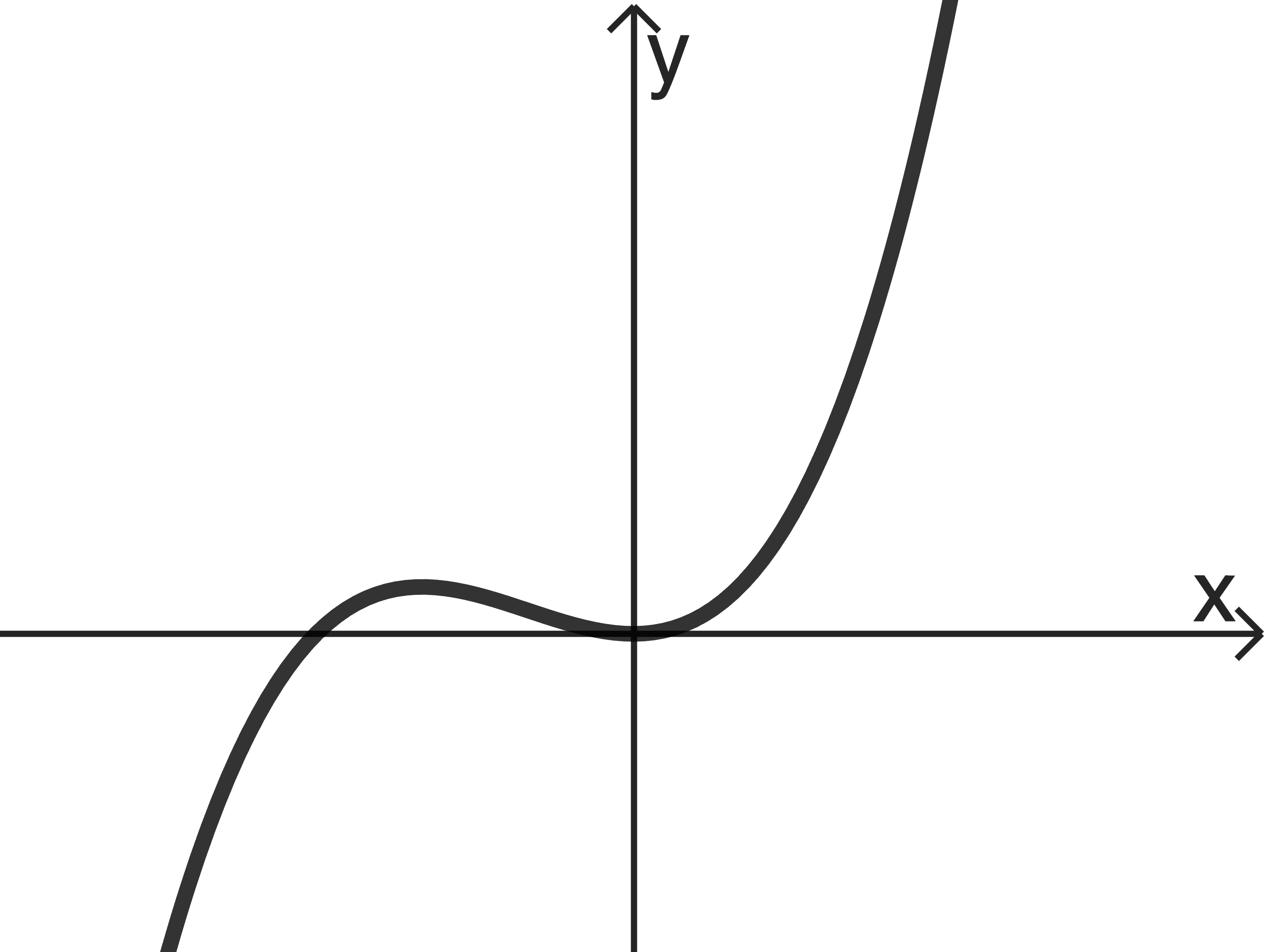
(1 BE)
- Details
- Kategorie: Analysis 2
Berechnen Sie den Inhalt der Fläche, die der Graph von \(g\) mit der \(x\)-Achse einschließt.
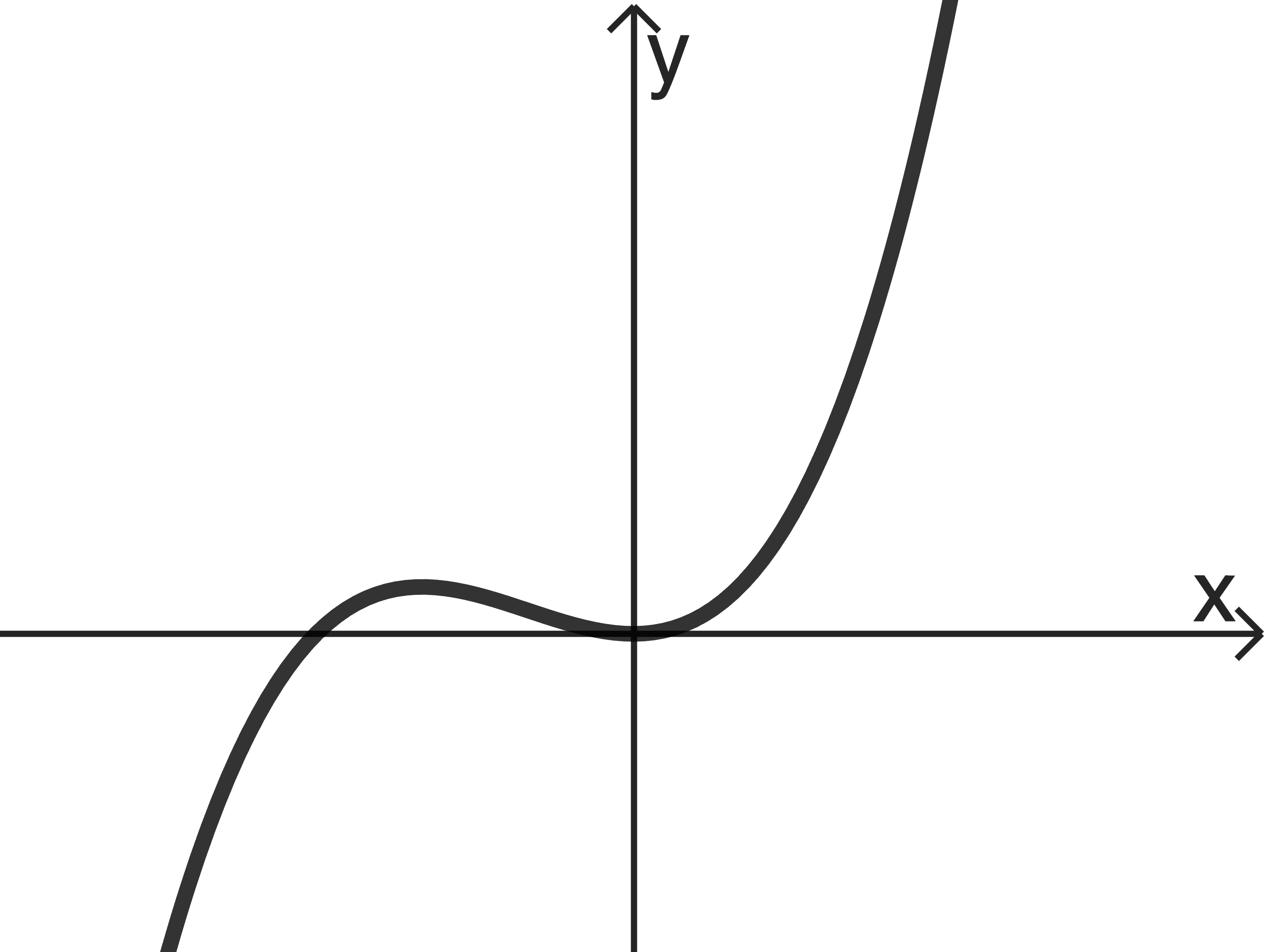Abb. 1
(4 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die in \([-3;+\infty[\) definierte Funktion \(h \colon x \mapsto \sqrt{x+3}-2\).
Beschreiben Sie, wie der Graph von \(h\) aus dem Graphen der in \(\mathbb R_0^+\) definierten Funktion \(w \colon x \mapsto \sqrt{x}\) hervorgeht.
(2 BE)
- Details
- Kategorie: Analysis 2
Begründen Sie, dass \(h\) umkehrbar ist, und beschreiben Sie, wie der Graph der Umkehrfunktion \(h^{-1}\) von \(h\) aus dem Graphen von \(h\) hervorgeht. Geben Sie den Definitions- und den Wertebereich von \(h^{-1}\) an.
(4 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist für jede positive reelle Zahl a die in \(\mathbb R\) definierte Funktion \(f_a\) mit \(f_a(x) = ax^2\). Abbildung 2 zeigt den Graphen von \(f_{\frac{1}{2}}\) sowie die Tangente \(t\) an den Graphen von \(f_{\frac{1}{2}}\) im Punkt \(\big(4 \big| f_{\frac{1}{2}}(4) \big)\).
Geben Sie anhand von Abbildung 2 eine Gleichung der Tangente \(t\) an.
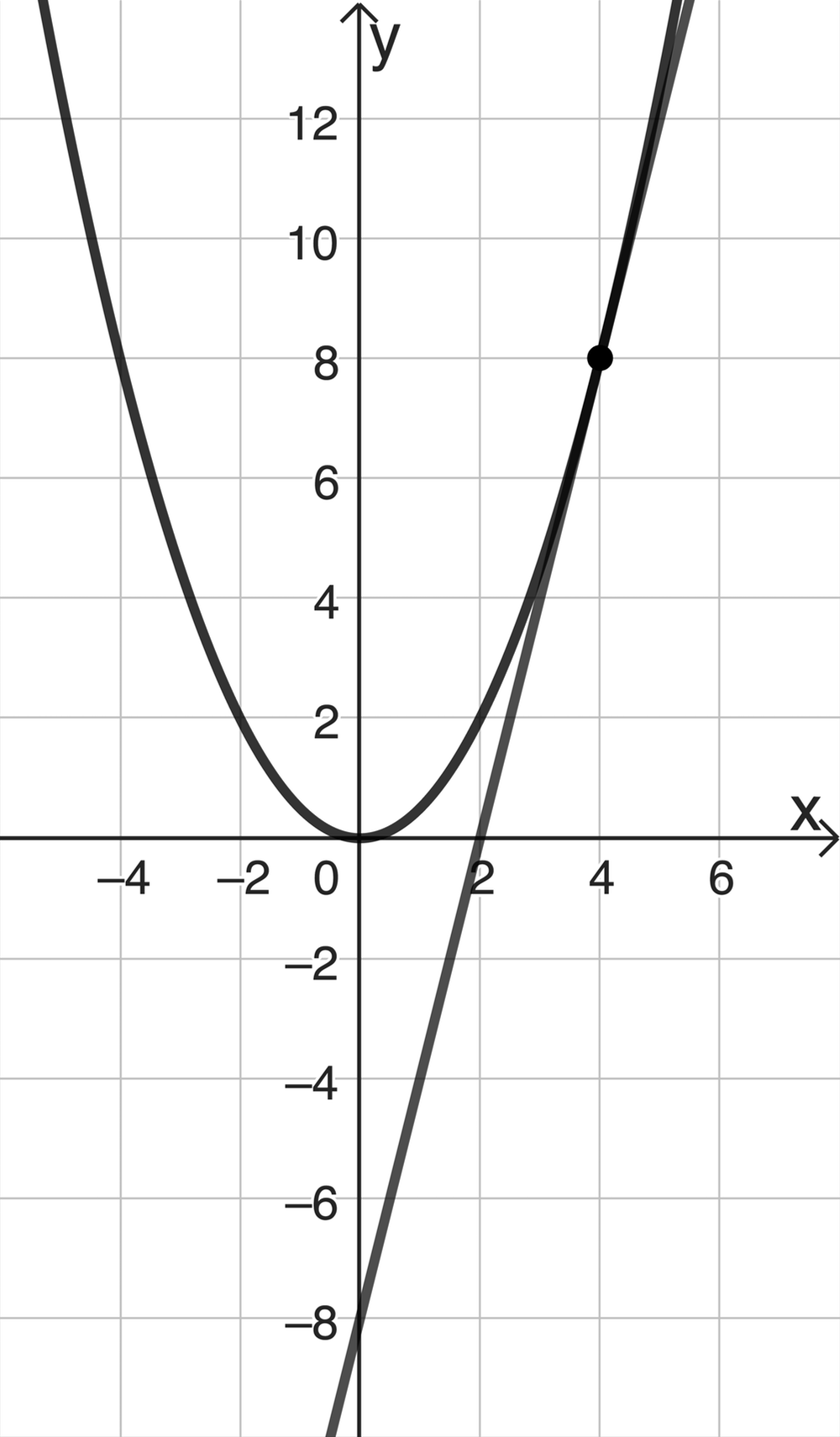
(1 BE)
- Details
- Kategorie: Analysis 2
Weisen Sie nach, dass für jeden Wert \(u \in \mathbb R\) die Tangente an den Graphen von \(f_a\) im Punkt \((u|f_a(u))\) die \(y\)-Achse im Punkt \((0|-f_a(u))\) schneidet.
(4 BE)
