- Details
- Kategorie: Analysis 1
Gegeben ist die Funktion \(f \colon x \mapsto \ln{(x - 3)}\) mit maximaler Definitionsmenge \(D\) und Ableitungsfunktion \(f'\).
Geben Sie \(D\) sowie die Nullstelle von \(f\) an.
(2 BE)
- Details
- Kategorie: Analysis 1
Ermitteln Sie diejenige Stelle \(x \in D\), für die \(f'(x) = 2\) gilt.
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R \backslash \{0\}\) definierte Funktion \(g \colon x \mapsto \dfrac{1}{x^2} - 1\).
Geben Sie eine Gleichung der waagrechten Asymptote des Graphen von \(g\) sowie die Wertemenge von \(g\) an.
(2 BE)
- Details
- Kategorie: Analysis 1
Berechnen Sie den Wert des Integrals \(\displaystyle \int_{\frac{1}{2}}^{2}g(x)dx\).
(3 BE)
- Details
- Kategorie: Analysis 1
Eine in \(\mathbb R\) definierte ganzrationale, nicht lineare Funktion \(f\) mit erster Ableitungsfunktion \(f'\) und zweiter Ableitungsfunktion \(f''\) hat folgende Eigenschaften:
- \(f\) hat bei \(x_1\) eine Nullstelle.
- Es gilt \(f'(x_2) = 0\) und \(f''(x_2) \neq 0\).
- \(f'\) hat ein lokales Minimum an der Stelle \(x_3\).
Abbildung 1 zeigt die Positionen von \(x_1\), \(x_2\) und \(x_3\).
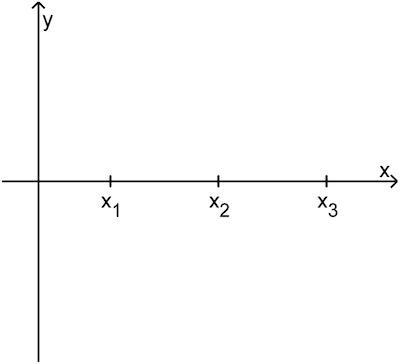Abb. 1
Begründen Sie, dass der Grad von \(f\) mindestens 3 ist.
(2 BE)
- Details
- Kategorie: Analysis 1
Skizzieren Sie in Abbildung 1 einen möglichen Graphen von \(f\).
(3 BE)
- Details
- Kategorie: Analysis 1
Abbildung 2 zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(g\), dessen einzige Extrempunkte \((-1|1)\) und \((0|0)\) sind, sowie den Punkt \(P\).
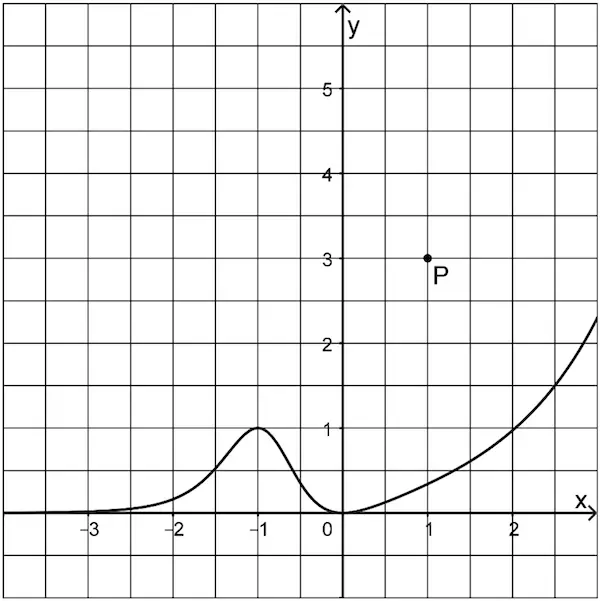Abb. 2
Geben Sie die Koordinaten des Tiefpunkts des Graphen der in \(\mathbb R\) definierten Funktion \(h(x) = -g(x - 3)\) an.
(2 BE)
- Details
- Kategorie: Analysis 1
Der Graph einer Stammfunktion von \(g\) verläuft durch \(P\). Skizzieren Sie diesen Graphen in Abbildung 2.
(3 BE)
